Câu 1 (1,5 điểm).
a) Tính $\underset{x\to -\infty }{\mathop{\lim }}\,\dfrac{4x+1}{-x+1}$.
b) Tìm giá trị thực của tham số $m$ để hàm số $f\left( x \right)=\left\{ \begin{aligned} & \dfrac{{{x}^{2}}-x-2}{x-2}\,\,\text{khi}\,\,x\ne 2 \\ & m\,\,\text{khi}\,\,x=2 \\ \end{aligned} \right.$ liên tục tại $x=2$.

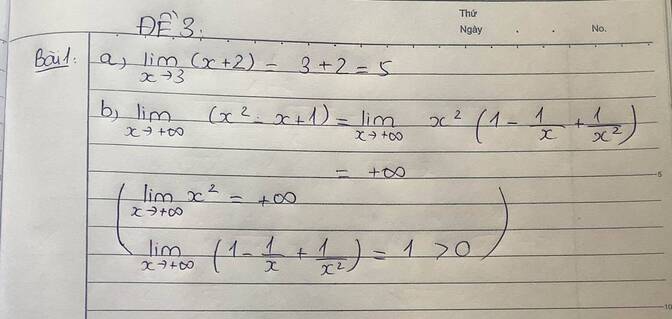


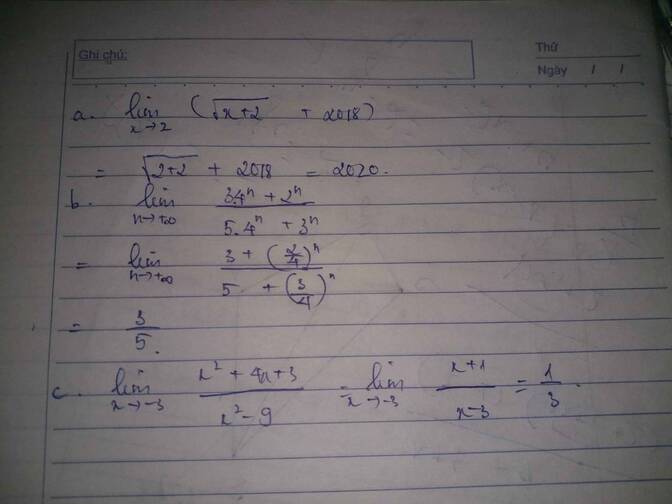
a) Ta có \(\lim\limits_{x\rightarrow-\infty}\dfrac{4x+1}{-x+1}=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{-4+\dfrac{1}{x}}{1+\dfrac{1}{x}}\right)=-4\)
b) Ta có \(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2-x-2}{x-2}=\lim\limits_{x\rightarrow2}\left(\dfrac{\left(x+1\right)\left(x-2\right)}{x-2}\right)\)
\(=\lim\limits_{x\rightarrow2}\left(x+1\right)=2+1=3\)
Để hàm số đã cho liên tục tại \(x=2\) thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)=m\) hay \(m=3\).