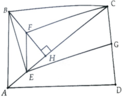
cho hình chữ nhật ABCD. Qua B kẻ đường thẳng vuông góc với đường chéo AC tại H. Gọi E,F,G theo thứ ự là trung điểm của AH,BH và CD
a) chứng minh tứ giác EFCG là hình bình hành.
b) Chứng minh góc BEG=90 độ
c) cho BH=h; Góc BAC=α. Tính đường chéo AC và diện tích hình chữ nhật ABCD theo h và α

a) EF là đường trung bình của tam giác ABH => EF//AB; EF=1/2AB (1)
Có G là trung điểm của DC => GC//AB(DC//AB); GC=1/2AB(DC=AB) (2)
Từ (1)$(2) => EF//GC; EF=GC => Tứ giác EFCG là hình bình hành.
b) Xét tam giác EBH và tam giác CBH có:BH là cạnh chung
EHB=CHB=90 (gt)
EH=EC(H là trung điểm của EC)
Vậy tam giác EBH=tam giac CBH (cgv-cgv)
=>BEH=BCH ; EBH=CBH
Lại có:BEH+EBH+BCH+CBH=180 =>BEH=EBH=BCH=CBH=180/4=45 (3)
Co BCE+ECG=BCG
Ma BCG=90(ABCD là hcn); BCE=45(cmt)
=> ECG=45
Xét tam giác EGC có:EGC+GEC+ECG=180
=> EGC=180-(GEC+ECG)
=180-(90+45)=45 (4)
Tu (3)$(4) => BEG=90
c)Tu CM