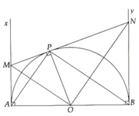
Cho nửa đường tròn tâm O, đường kính AB=2R. Vẽ dây AC: góc BAC =30 độ
a) Tính chu vi tam giác ABC theo R
b) trên tia tiếp tuyến Ax với nửa đường tròn, Lấy D: AD= 2HC (CH là đường cao tam giác ABC). Tính góc D và góc tạo bởi 2 bán kính OA, OC
c) c/m CD là tiếp tuyến của đường tròn

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C có \(sinCAB=\dfrac{CB}{AB}\)
=>\(\dfrac{CB}{2R}=sin30=\dfrac{1}{2}\)
=>CB=R
Xét ΔCAB vuông tại C có \(CB^2+CA^2=AB^2\)
=>\(CA^2+R^2=\left(2R\right)^2=4R^2\)
=>\(CA^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Chu vi tam giác ABC là:
\(C_{ABC}=CA+CB+AB=R+2R+R\sqrt{3}=R\left(3+\sqrt{3}\right)\)
b: Xét ΔCHA vuông tại H có \(sinCAH=\dfrac{CH}{CA}\)
=>\(\dfrac{CH}{R\sqrt{3}}=sin30=\dfrac{1}{2}\)
=>\(CH=\dfrac{R\sqrt{3}}{2}\)
Ta có: DA=2CH
=>\(DA=2\cdot\dfrac{R\sqrt{3}}{2}=R\sqrt{3}\)
Ta có: \(\widehat{DAC}+\widehat{CAB}=90^0\)
=>\(\widehat{DAC}=90^0-\widehat{CAB}=90^0-30^0=60^0\)
Xét ΔADC có \(AD=AC\left(=R\sqrt{3}\right)\) và \(\widehat{DAC}=60^0\)
nên ΔADC đều
=>\(\widehat{D}=60^0\)
Xét ΔOAC có OA=OC
nên ΔOAC cân tại O
=>\(\widehat{AOC}=180^0-2\cdot\widehat{OAC}=180^0-2\cdot30^0=120^0\)
c: Xét tứ giác DAOC có \(\widehat{DAO}+\widehat{DCO}+\widehat{ADC}+\widehat{AOC}=360^0\)
=>\(\widehat{DCO}+90^0+120^0+60^0=360^0\)
=>\(\widehat{DCO}=90^0\)
=>CD là tiếp tuyến của (O)