1.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A',B' lần lượt là trung điểm của SA,SB . Đường thẳng A' B' song song với mặt phẳng nào dưới đây?
A. (SAB).
B. ( ABCD) .
C. (SAD).
D. (SBC).
2.Cho hình hộp ABCD.A' B' C' D' . Mặt phẳng ( ABA') song song với:
A. ( AA'C') .
B. (CC'D').
C. ( ADD').
D. (BB'A').
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C

Vì CD ⊂ (MCD), CD // AB, AB ⊂ (SAB) nên giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB. Vậy MN // CD. Hơn nữa MN ≠ CD. Vậy thiết diện là hình thang CNMD.
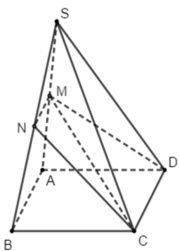
Đáp án C

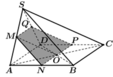
Tham khảo hình vẽ bên.
Gọi P, Q lần lượt là trung điểm của CD, SD. Khi đó thiết diện tạo bởi mặt phẳng (OMN) với hình chóp là hình thang MNPQ. Thật vậy:
![]()
Chọn B.

Đáp án D
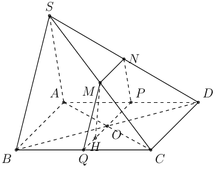
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .
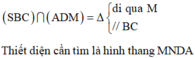
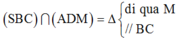
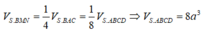
Câu 1: B
Câu 2: B