Bài 5 : Cho \(\Delta ABC\) có AB = AC , lấy M là trung điểm của BC . Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD = CE . Chứng minh :b )\(\Delta ABD=\Delta ACE\) a ) AM vuông góc với BC c )\(\Delta ACD=\Delta ABE\) d ) AM là tia phân giác của góc DAEBài 6 : Cho tam giác ABC ( AC > AB ) . Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy E sao cho AE = AB .a ) Chứng minh BD = DEb )...
Đọc tiếp
Bài 5 : Cho \(\Delta ABC\) có AB = AC , lấy M là trung điểm của BC . Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD = CE . Chứng minh :
b )\(\Delta ABD=\Delta ACE\) a ) AM vuông góc với BC
c )\(\Delta ACD=\Delta ABE\) d ) AM là tia phân giác của góc DAE
Bài 6 : Cho tam giác ABC ( AC > AB ) . Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy E sao cho AE = AB .
a ) Chứng minh BD = DE
b ) Kéo dài AB và DE cắt nhau tại K. Chứng minh góc AKD bằng góc ACD .
c ) Chứng minh \(\Delta KBE=\Delta CEB\)
d ) Tìm điều kiện của tam giác ABC để DE vuông góc với AC .
Bài 7 Cho tam giác ABC , P là trung điểm của AB . Đường thẳng qua P và song song với BC cắt AC ở đường thẳng qua Q và song song với AB cắt BC ở F. Chứng minh rằng :
a ) AP = QF
b ) \(\Delta APQ=\Delta QFC\)
c ) Q là trung điểm của AC
d ) Lấy điểm I thuộc tia đối của tia QP sao cho QI = QP . Chứng minh CI // AB
Bài 8 : Cho đoạn thẳng AB . Trên hai nửa mặt phẳng đối nhau bờ AB , kẻ tia Ax và By cùng vuông góc với AB . Trên tia Ax , By lần lượt lấy hai điểm C , D sao cho AC = BD .
a ) Chứng minh AD = BC
. b ) Chứng minh AD // BC .
c ) Gọi 0 là trung điểm của AB . Trên BC lấy điểm E , trên AD lấy điểm F sao cho CE = DF . Chứng minh ( là trung điểm của EF .
Mình đang cần gấp ạ

a: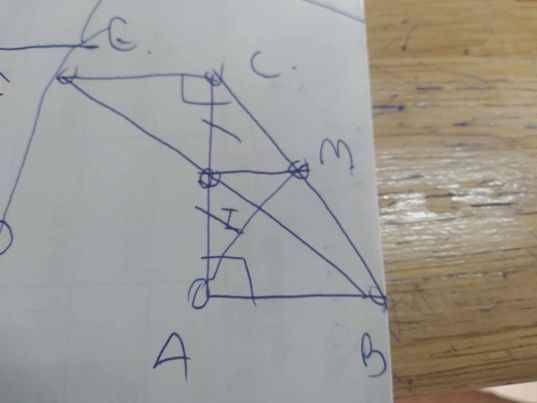
b:
Ta có: CE\(\perp\)CA
AB\(\perp\)CA
Do đó: CE//AB
Xét ΔCEB và ΔABE có
CE=AB
\(\widehat{CEB}=\widehat{ABE}\)(hai góc so le trong, AB//CE)
BE chung
Do đó: ΔCEB=ΔABE
=>CB=AE
Ta có: ΔCEB=ΔABE
=>\(\widehat{CBE}=\widehat{AEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên CB//AE
c: MI//CE
CE//AB
Do đó: MI//AB
Ta có: MI//AB
AB\(\perp\)AC
Do đó: MI\(\perp\)AC
Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
Ta có: ΔMAC cân tại M
mà MI là đường cao
nên MI là phân giác của \(\widehat{AMC}\)
d: Ta có: \(\widehat{MAC}+\widehat{MAB}=\widehat{BAC}=90^0\)
\(\widehat{MCA}+\widehat{MBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{MAC}=\widehat{MCA}\)(ΔAMC cân tại M)
nên \(\widehat{MAB}=\widehat{MBA}\)
=>ΔMAB cân tại M
Xét ΔMAB cân tại M có \(\widehat{MBA}=60^0\)
nên ΔMAB đều
=>\(\widehat{BAM}=60^0\)
e: Xét ΔECI vuông tại C và ΔBAI vuông tại A có
EC=BA
CI=AI
Do đó:ΔECI=ΔBAI
=>\(\widehat{EIC}=\widehat{BIA}\)
mà \(\widehat{EIC}+\widehat{EIA}=180^0\)(hai góc kề bù)
nên \(\widehat{EIA}+\widehat{BIA}=180^0\)
=>B,I,E thẳng hàng