Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

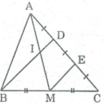
Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).

Gọi K là trung điểm của DC
Suy ra: AD=DK=KC
Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của DC
Do đó: MK là đường trung bình của ΔBDC
Suy ra: MK//BD và \(MK=\dfrac{BD}{2}\)
hay ID//MK
Xét ΔAMK có
D là trung điểm của AK
DI//MK
Do đó: I là trung điểm của AM
hay IA=IM

a) Xét tam giác BDC có:
M là trung điểm BC(gt)
E là trung điểm DC(DE=EC)
=> ME là đường trung bình
=> ME//BD
b) Xét tam giác AME có:
ME//BD
D là trung điểm AE(AD=DE)
=> I là trung điểm AM
c) Xét tam giác AME có:
D là trung điểm AE(AD=DE)
I là trung điểm AM(cmt)
=> ID là đường trung bình
\(\Rightarrow ID=\dfrac{1}{2}ME\)
Mà \(ME=\dfrac{1}{2}BD\)(do ME là đường trung bình tam giác BDC)
\(\Rightarrow ID=\dfrac{1}{2}.\dfrac{1}{2}BD=\dfrac{1}{4}BD\)

Hình bạn tự vẽ nhé
Giải: Kẻ \(MG//BD\) ta có: \(\hept{\begin{cases}MG//BD\\MB=MC\left(gt\right)\end{cases}}\Rightarrow\) MG là đường trung bình tam giác BCD.
\(\Rightarrow DG=CG=\frac{1}{2}CD\Rightarrow DG=AD\)
Xét tam giác AMG ta có: \(\hept{\begin{cases}MG//DI\\AD=DG\end{cases}}\Rightarrow AI=IM\left(đpcm\right)\) (tc đường tb tam giác)

a) Xét △ AED có AE=AD nến △AED cân tại A
⇒\(\widehat{AED}=\widehat{ADE}\) ⇒\(\widehat{DEB}=\widehat{EDC}\)
△ABC cân ⇒AB=AC mà AE=AD⇒EB=DC
Xét △DEB và △EDC có :
\(\widehat{DEB}=\widehat{EDC}\left(cmt\right)\)
ED : cạnh chung
EB=DC \(\left(cmt\right)\)
Do đó : △DEB = △EDC \(\left(c.g.c\right)\)
Nên \(\widehat{EBD}=\widehat{DCE}\) hay \(\widehat{ABD}=\widehat{ACE}\)
b) △ABC cân ⇒\(\widehat{ABC}=\widehat{ACB}\) mà \(\widehat{ABD}=\widehat{ACE}\) (câu a) ⇒\(\widehat{IBC}=\widehat{ICB}\)
Vậy △IBC cân tại I
c) Xét △AIB và △AIC có :
AB=AC(gt)
\(\widehat{ABD}=\widehat{ACE}\) (câu a)
BI=CI(vì △IBC cân tại I)
Do đó :△AIB=△AIC\(\left(c.g.c\right)\)
⇒\(\widehat{BAI}=\widehat{CAI}\) ⇒ AI là tia phân giác \(\widehat{BAC}\)
d) Xét △AED và △ABC có :
A : chung
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Nên △AED đồng dạng △ABC \(\left(c.g.c\right)\)
⇒\(\widehat{AED}=\widehat{ABC}\) ⇒ ED//BC
Vì AI là đường phân giác của △AED mà △AED cân nên AI cũng là đường cao ⇒AI⊥ED lại có : ED//BC ⇒AI⊥BC
e) AI⊥BC (AI là đường cao tam giác ABC) mà △ABC cân nên AI cũng là đường trung tuyến ⇒ AI là đường trung trực của BC
a, Xét tam giác ABD và tam giác ACE ta có :
^A _ chung
^AB = AC ( gt )
AD = AE ( gt )
Vậy tam giác ABD = tam giác ACE ( g.c.g )
b, => ^ABD = ^ACE ( 2 góc tương ứng )
mà tam giác ABC cân tại => ^B = ^C
=> ^B - ^ABD = ^DBC
=> ^C - ^ACE = ^ECB
=> ^DBC = ^ECB
Xét tam giác IBC có : ^DBC = ^ECB
nên IBC là tam giác cân tại I
c, Xét tam giác ABI và tam giác ACI ta có :
^ABI = ^ACI ( cmt )
AB = AC ( gt)
IA _ chung
Vậy tam giác ABI = tam giác ACI ( c.g.c )
=> ^BAI = ^CAI ( 2 góc tương ứng )
Vậy AI là phân giác ^BAC
d, Ta có : \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)=> ED // BC ( Ta lét đảo )
mà AI là phân giác của tam giác ABC cân tại A
=> AI đồng thời là đường cao
=> AI vuông BC ; ED // BC (cmt)
=> AI vuông ED
e, Xét tam giác ABC cân tại A
AI là đường cao, phân giác
đồng thời AI là đường trung trực đoạn BC

Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).

Lấy N là trung điểm của DC ; ta có \(AD=DN=NC\)
Xét tam giác BCD có MN là đường trung bình \(\Rightarrow MN\text{//}BD\) hay \(MN\text{//}ID\)
Xét tam giác AMN có D là trung điểm của AN; ID//MN (cmt) => I là trung điểm của AM
=> ĐPCM

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
=>BE=DC
=>AE=AD
b: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
=>ΔAEI=ΔADI
=>góc EAI=góc DAI
=>AI là phân giác của góc BAC
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
=>A,I,M thẳng hàng
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `2\Delta` vuông và `BEC` và `CDB`:
`\text {BC chung}`
$\widehat {B} = \widehat {C}$
`=> \Delta BEC = \Delta CDB (ch-gn)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AE + BE}\\\text{AC = AD + CD}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BE = CD}\end{matrix}\right.\)
`-> \text {AE = AD}`
Xét `2\Delta` vuông `AEI` và ` ADI`:
`\text {AE = AD}`
`\text {AI chung}`
`=> \Delta AEI = \Delta ADI (ch-cgv)`
`->` $\widehat {EAI} = \widehat {DAI} (\text {2 góc tương ứng})$
`-> \text {AI là tia phân giác của}` $\widehat {EAD}$
Mà \(\text{E}\in\text{AB, D}\in\text{AC}\)
`-> \text {AI là tia phân giác của}` $\widehat {BAC}$ `(1)`
`c,`
Vì M là trung điểm của AC
`-> \text {AM là đường trung tuyến của} \Delta ABC` `(2)`
Từ `(1)` và `(2)`
`-> \text {Ba điểm A, I, M thẳng hàng.}`
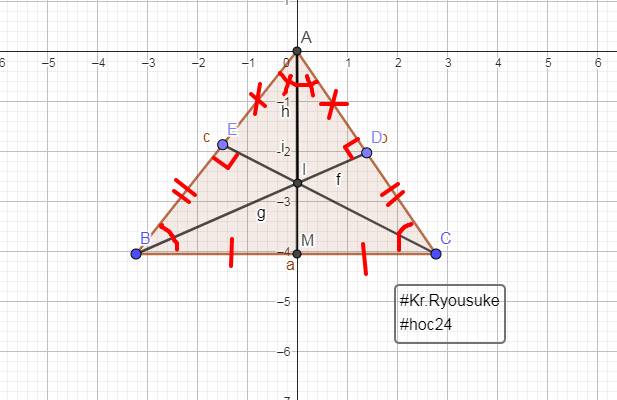
a: Ta có: AD=DE=EC
=>D là trung điểm của AE và E là trung điểm của DC
Xét ΔBDC có
M,E lần lượt là trung điểm của CB,CD
=>ME là đường trung bình của ΔBDC
=>ME//BD
b: Ta có: ME//BD
I\(\in\)BD
Do đó: ID//ME
Xét ΔAME có
D là trung điểm của AE
DI//ME
Do đó: I là trung điểm của AM
=>AI=IM