 giải dùm em bài 4 với ạ
giải dùm em bài 4 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



4:
a: vì a=2>0
nên hàm số y=2x-1 đồng biến trên R
b:
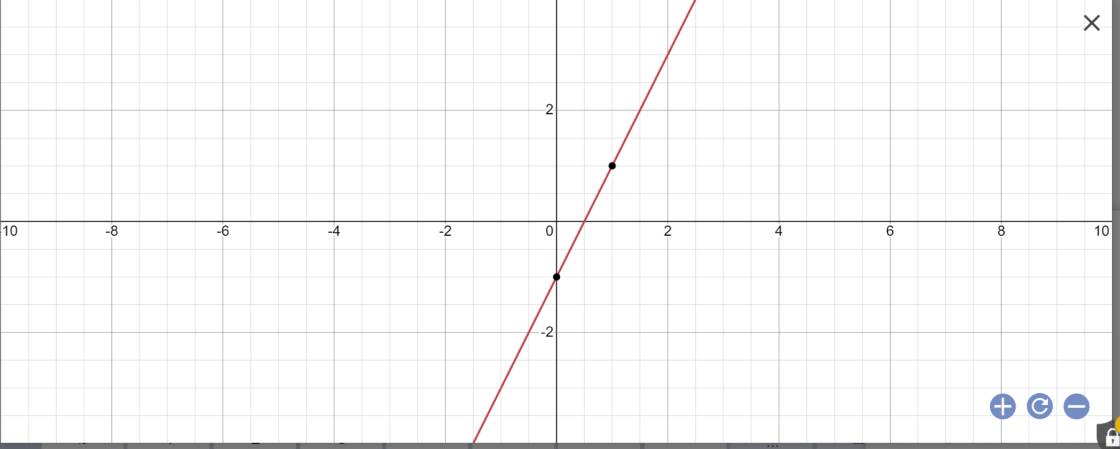
c: Thay x=1 vào y=2x-1, ta được:
\(y=2\cdot1-1=2-1=1\)
=>A(1;1) có thuộc (d)
d: Phương trình hoành độ giao điểm là:
2x-1=-x+2
=>\(2x+x=2+1\)
=>3x=3
=>x=1
Thay x=1 vào y=2x-1, ta được:
\(y=2\cdot1-1=1\)
Vậy: (d) cắt (d') tại A(1;1)
e: Vì (m): y=ax+b song song với (d) nên ta có:
\(\left\{{}\begin{matrix}a=2\\b< >-1\end{matrix}\right.\)
=>y=2x+b
Thay x=-2 và y=3 vào y=2x+b, ta được:
b-2*2=3
=>b-4=3
=>b=7
=>y=2x+7

Bài 1:
a, \(Mg\left(OH\right)_2\underrightarrow{t^o}MgO+H_2O\)
b, \(Fe_2O_3+6HNO_3\rightarrow2Fe\left(NO_3\right)_3+3H_2O\)
c, \(BaCO_3+2HCl\rightarrow BaCl_2+H_2O+CO_2\)
d, \(CO_2+KOH\rightarrow KHCO_3\)
Bài 2:
_ Trích mẫu thử.
_ Cho lần lượt từng mẫu thử tác dụng với dd H2SO4.
+ Nếu có khí thoát ra, đó là K2CO3.
PT: \(K_2CO_3+H_2SO_4\rightarrow K_2SO_4+H_2O+CO_2\)
+ Nếu xuất hiện kết tủa trắng và có khí thoát ra, đó là BaCO3.
PT: \(BaCO_3+H_2SO_4\rightarrow BaSO_{4\downarrow}+H_2O+CO_2\)
+ Nếu không có hiện tượng, đó là BaSO4.
_ Dán nhãn.
Bạn tham khảo nhé!

9.
Gọi H là trung điểm AB \(\Rightarrow A'H\perp\left(ABCD\right)\Rightarrow\widehat{A'CH}=45^0\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\dfrac{2a}{2}\right)^2+a^2}=a\sqrt{2}\)
\(\Rightarrow A'H=CH.tan45^0=a\sqrt{2}\)
\(V=A'H.AB.AD=2a^3\sqrt{2}\)
b.
Ta có: \(DD'||AA'\Rightarrow DD'||\left(AA'C\right)\)
\(\Rightarrow d\left(DD';A'C\right)=d\left(DD';\left(AA'C\right)\right)=d\left(D;\left(AA'C\right)\right)\)
Trong mp (ABCD), nối DH cắt AC tại E \(\Rightarrow DH\cap\left(AA'C\right)=E\)
Áp dụng định lý Talet: \(\dfrac{EH}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow DE=2EH\)
\(\Rightarrow d\left(D;\left(AA'C\right)\right)=2d\left(H;\left(AA'C\right)\right)\)
Kẻ \(HF\perp AC\Rightarrow AC\perp\left(AHF\right)\)
Trong tam giác vuông AHF, kẻ \(HK\perp A'F\Rightarrow HK\perp\left(AA'C\right)\Rightarrow HK=d\left(H;\left(AA'C\right)\right)\)
Ta có: \(HF=AH.sin\widehat{BAC}=\dfrac{AH.BC}{AC}=\dfrac{AH.BC}{\sqrt{AB^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{HF^2}+\dfrac{1}{A'H^2}=\dfrac{11}{2a^2}\Rightarrow HK=\dfrac{a\sqrt{22}}{11}\)
\(\Rightarrow d\left(DD';A'C\right)=2HK=\dfrac{2a\sqrt{22}}{11}\)



\(\left(m+1\right)^2\ge4m\Leftrightarrow m^2+2m+1\ge4m\Leftrightarrow m^2-2m+1\ge0\)\(\Leftrightarrow\left(m-1\right)^2\ge0\)
Vì \(\left(m-1\right)^2\ge0\)(luôn đúng) nên pt vô số nghiêmj
Mình cũng ko bt đây là giải pt hay cm BĐT nữa nên nếu ko đúng mục đích thì bạn thông cảm

Bài 6:
a. Sai. Vì $x^2=\frac{1}{3}\Leftrightarrow x=\pm \sqrt{\frac{1}{3}}$ là số vô tỉ.
Mệnh đề phủ định: $\forall x\in\mathbb{Q}, 9x^2-3\neq 0$
b. Sai. Cho $n=0$ thấy $n^2+1=1$ không chia hết cho $8$
Mệnh đề phủ định: $\exists x\in\mathbb{N}| n^2+1\not\vdots 8$
c. Sai. Cho $x=1$ thấy sai.
Phủ định: \(\exists c\in\mathbb{R}| (x-1)^2=x-1\)
d. Sai, cho $n=0$ thấy sai.
Phủ định: $\exists n\in\mathbb{N}| n^2\leq n$
Bài 4:
a.
$x^2-5x+4=0$
$\Leftrightarrow (x-1)(x-4)=0$
$\Leftrightarrow x=1$ hoặc $x=4$
b.
$x^2-5x+6=0$
$\Leftrightarrow (x-2)(x-3)=0$
$\Leftrightarrow x=2$ hoặc $x=3$
c.
$x^2-3x>0$
$\Leftrightarrow x(x-3)>0$
$\Leftrightarrow x>3$ hoặc $x< 0$
d. ĐK $x\geq 0$
$\sqrt{x}=x$
$\Leftrightarrow \sqrt{x}(\sqrt{x}-1)=0$
$\Leftrightarrow x=0$ hoặc $x=1$
e.
$2x+3\leq 7$
$\Leftrightarrow 2x\leq 4$
$\Leftrightarrow x\leq 2$
f.
$x^2+x+1>0$
$\Leftrightarrow (x+\frac{1}{2})^2+\frac{3}{4}>0$
$\Leftrightarrow x\in\mathbb{R}$

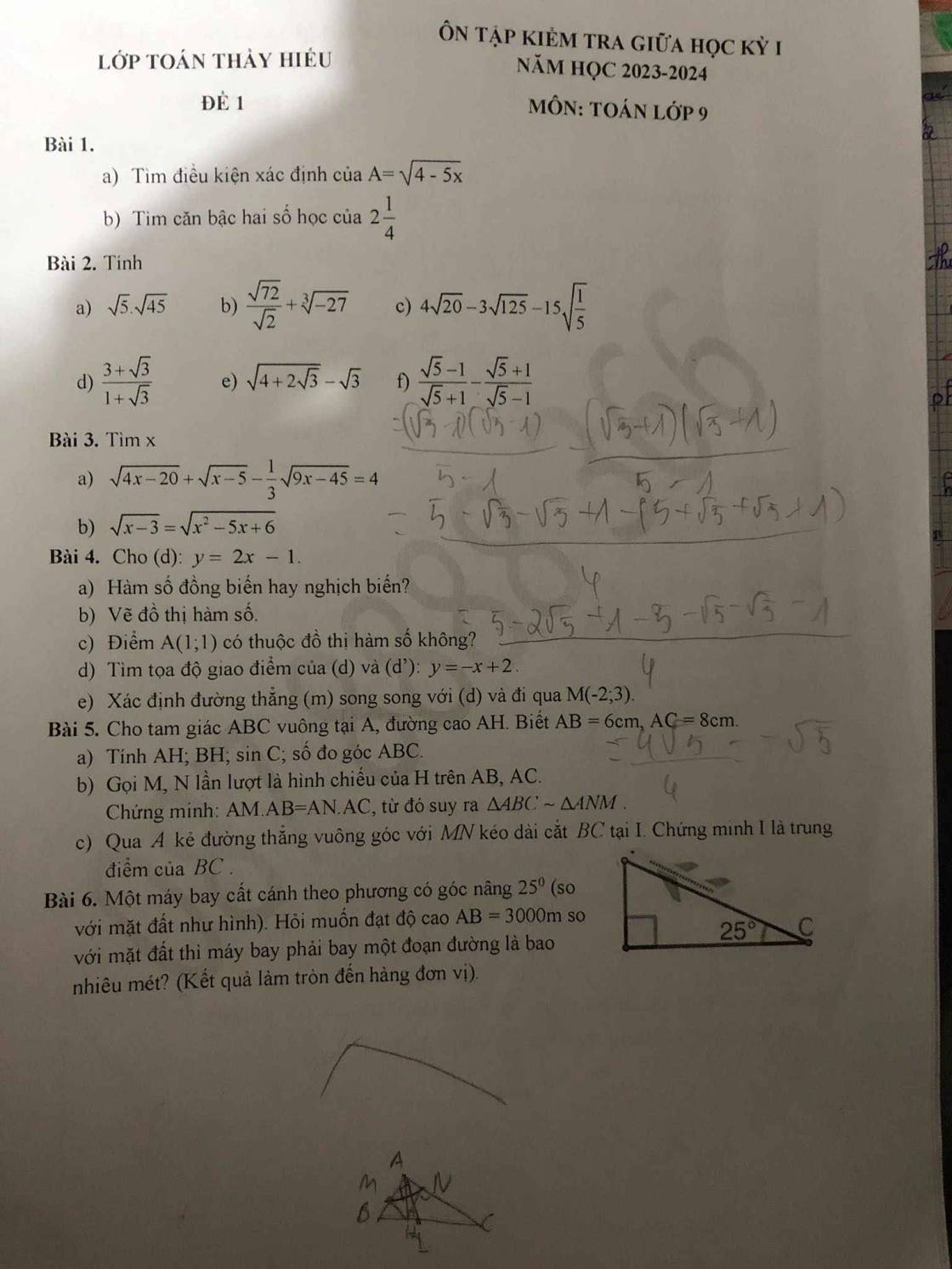
 Giải dùm em bài 1,2,3,4,5 với ạ
Giải dùm em bài 1,2,3,4,5 với ạ




Câu d nữa anh ơi