Cho đường tròn \(\left(O\right)\) và điểm \(A\) bên ngoài đường tròn, từ \(A\) vẽ tiếp tuyến \(AB\) với đường tròn (\(B\) là tiếp điểm). Kẻ đường kính \(BC\) của đường tròn \(\left(O\right)\). \(AC\) cắt đường tròn \(\left(O\right)\) tại \(D\) (\(D\) khác \(C\)).
\(a\)) Chứng minh \(BD\) vuông góc \(AC\) và \(AB^2=AD\cdot AC\).
\(b\)) Từ \(C\) vẽ dây \(CE//OA,BE\) cắt \(OA\) tại \(H\). Chứng minh \(H\) là trung điểm \(BE\) và \(AE\) là tiếp tuyến của đường tròn \(\left(O\right)\).
\(c\)) Tia \(OA\) cắt đường tròn \(\left(O\right)\) tại \(F\). Chứng minh \(FA\cdot CH=HF\cdot CA\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

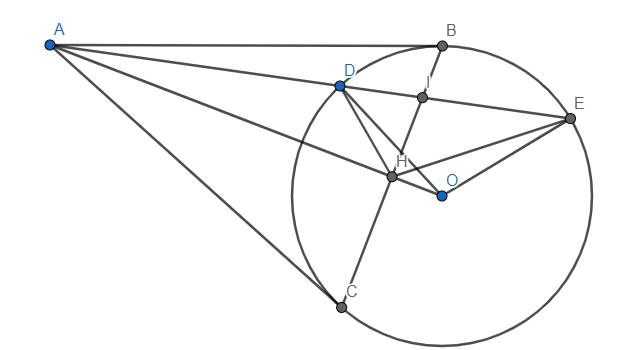
a) Do AB, AC tiếp xúc (O) tại B, C nên \(\widehat{OBA}=90^o\) và \(OA\perp BC\) tại H.
Xét tam giác OAB vuông tại B có đường cao BH, ta có \(OB^2=OA.OH\)
Mà \(OB=OD\left(=R_{\left(O\right)}\right)\) nên \(OD^2=OA.OH\). Từ đó suy ra \(\dfrac{OD}{OA}=\dfrac{OH}{OD}\). Từ đó dễ dàng suy ra 2 tam giác OHD và ODA đồng dạng.
b) Tam giác OAB vuông tại B có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, ta có \(\widehat{ABD}=\widehat{AEB}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung BD.
\(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
Từ đó suy ra \(AH.AO=AD.AE\) hay \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\). Do đó \(\Delta AHE~\Delta ADO\left(c.g.c\right)\) \(\Rightarrow\widehat{AEH}=\widehat{AOD}\) hay tứ giác OHDE nội tiếp.
\(\Rightarrow\widehat{AHD}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\)
\(\Rightarrow90^o-\widehat{AHD}=90^o-\widehat{OHE}\) \(\Rightarrow\widehat{DHI}=\widehat{EHI}\).
Ta suy ra được đpcm.

a) Xét tứ giác OBAC có
\(\widehat{OBA}\) và \(\widehat{OCA}\) là hai góc đối
\(\widehat{OBA}+\widehat{OCA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OBAC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

1: \(AO=\sqrt{3^2+8^2}=\sqrt{73}\left(cm\right)\)
BC=2*R=6cm
\(CA=\sqrt{AB^2+BC^2}=\sqrt{8^2+6^2}=10\left(cm\right)\)
BD=6*8/10=4,8cm
2: Xét ΔBCE có
O là trung điểm của BC
OH//CE
=>H là trung điểm của BE
ΔOBE cân tại O
mà OH là trung tuyến
nên OH là phân giác của góc BOE
Xét ΔOBA và ΔOEA có
OB=OE
góc BOA=góc EOA
OA chung
=>ΔOBA=ΔOEA
=>góc OEA=90 độ
=>AE là tiếp tuyến của (O)

a: ΔODE cân tại O
mà OM là trung tuyến
nên OM vuông góc DE
=>góc OMA=90 độ=góc OCA=góc OBA
=>O,A,B,M,C cùng thuộc 1 đường tròn
b: Xét ΔBSC và ΔCSD có
góc SBC=góc SCD
góc S chung
=>ΔBSC đồng dạng với ΔCSD
=>SB/CS=SC/SD
=>CS^2=SB*SD
góc DAS=gócEBD
=>góc DAS=góc ABD
=>ΔSAD đồng dạng với ΔSBA
=>SA/SB=SD/SA
=>SA^2=SB*SD=SC^2
=>SA=SC
c; BE//AC
=>EH/SA=BH/SC=HJ/JS
mà SA=SC
nênHB=EH
=>H,O,C thẳng hàng

a: Xét (O) có
ΔBDC nội tiếp đường tròn
BC là đường kính
DO đó:ΔBDC vuông tại D
Xét ΔBCA vuông tại B có BD là đường cao ứng với cạnh huyền AC
nên \(AB^2=AD\cdot AC\)