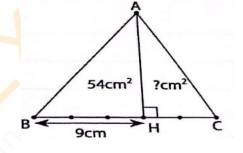
Cho tam giác ABC, đường cao AH (hình vẽ), biết BH = 9cm và HB = 3/2 HC. Tính diện tích tam giác AHC, biết diện tích tam giác AHB là 54cm2 . (tính theo 2 cách). Gợi ý: Cách 1: Áp dụng công thức Cách 2: Tính theo tỉ số tam giác.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(HB+HC=BC\)
=>\(\dfrac{1}{3}HC+HC=BC\)
=>\(BC=\dfrac{4}{3}HC\)
mà \(HB=\dfrac{1}{3}HC\)
nên \(\dfrac{BC}{HB}=\dfrac{4}{3}:\dfrac{1}{3}=4\)
=>BC=4HB
=>\(S_{ABC}=4\cdot S_{AHB}=4\cdot6=24\left(cm^2\right)\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/AB
=>BA^2=BH*BC
b: \(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
AC=căn 16*25=20(cm)
S=15*20/2=150cm2
c: AD/DC=HA/HC=12/16=3/4

tự vẽ hình
ta có <HBA+<BAH= 90\(^0\)(vì tam giác ABH vg tại H)
Có <BAH+ <HAC= 90\(^0\)(vì tam giác ABC vg tại A)
=> <HBA=<HAC
Xét tam giác BAH và ACH
<BHA=<AHC\(\left(90^0\right)\)
<ABH=<HAC
=> Tam giác BAH đồng dạng với tam giác ACH
=> BH/AH=AH/CH=> AH^2= BH*CH=4*9=36 cm
b, ta có BC=BH+CH=4+9=13 cm
S(ABC) = AH*BC=36*13=468 cm\(^2\)