help meeee

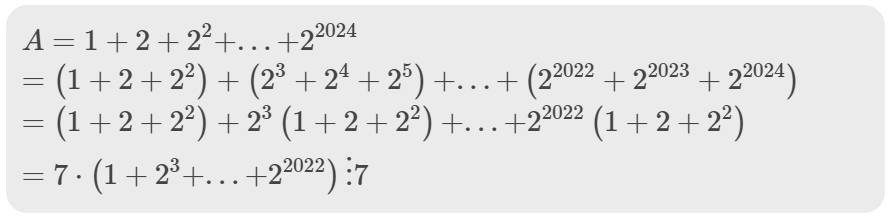
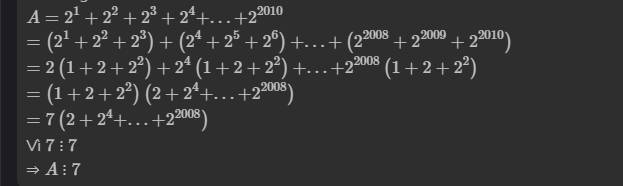
\(A=1+2+2^2+...+2^{2024}\)

\(=\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{2022}+2^{2023}+2^{2024}\right)\)

\(=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{2022}\left(1+2+2^2\right)\)

\(=7\cdot\left(1+2^3+...+2^{2022}\right)⋮7\)

1: \(A=6^{2020}\left(1+6\right)+6^{2022}\left(1+6\right)\)

\(=7\left(6^{2020}+6^{2022}\right)⋮7\)

Bài 1:

$A=6^{2020}(1+6+6^2+6^3)=6^{2020}.259=6^{2020}.7.37\vdots 7$

Ta có đpcm.

a) \(A=2+2^2+...+2^{2024}\)

\(2A=2^2+2^3+...+2^{2025}\)

\(2A-A=2^2+2^3+...+2^{2025}-2-2^2-...-2^{2024}\)

\(A=2^{2025}-2\) 

b) \(2A+4=2n\)

\(\Rightarrow2\cdot\left(2^{2025}-2\right)+4=2n\)

\(\Rightarrow2^{2026}-4+4=2n\)

\(\Rightarrow2n=2^{2026}\)

\(\Rightarrow n=2^{2026}:2\)

\(\Rightarrow n=2^{2025}\) 

c) \(A=2+2^2+2^3+...+2^{2024}\)

\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2023}+2^{2024}\right)\)

\(A=2\cdot3+2^3\cdot3+...+2^{2023}\cdot3\)

\(A=3\cdot\left(2+2^3+...+2^{2023}\right)\)

d) \(A=2+2^2+2^3+...+2^{2024}\)

\(A=2+\left(2^2+2^3+2^4\right)+\left(2^5+2^6+2^7\right)+...+\left(2^{2022}+2^{2023}+2^{2024}\right)\)

\(A=2+2^2\cdot7+2^5\cdot7+...+2^{2022}\cdot7\)

\(A=2+7\cdot\left(2^2+2^5+...+2^{2022}\right)\)

Mà: \(7\cdot\left(2^2+2^5+...+2^{2022}\right)\) ⋮ 7

⇒ A : 7 dư 2 

cái câu d nó cứ sao sao ý bn

Lời giải:

$A=9+2.3^2+2.3^3+2.3^4+...+2.3^{2023}$

$A-9=2(3^2+3^3+3^4+...+3^{2023})$

$3(A-9)=2(3^3+3^4+3^5+...+3^{2024})$

$\Rightarrow 3(A-9)-(A-9)=2(3^{2024}-3^2)$

$2(A-9)=2.3^{2024}-18$

$\Rightarrow 2A-18=2.3^{2024}-18$

$\Rightarrow A=3^{2024}\vdots 3^{2023}$ (đpcm)

tui lớp 8 ko bt làm :)

trời ơi cíu tui

1)  A=6²⁰²⁰+6²⁰²¹+6²⁰²²+6²⁰²³

    A= ( 6²⁰²⁰+6²⁰²¹) +  ( 6²⁰²²+6²⁰²³)

    A= 6²⁰²⁰.( 1+6) + 6²⁰²².( 1+6)

    A= 6²⁰²⁰.7+6²⁰²².7

    A= 7.( 6²⁰²⁰+6²⁰²²)

Vì 7 chia hết cho 7 => 7.(6²⁰²⁰+6²⁰²²) chia hết cho 7 hay A chia hết cho 7.

Vậy A chia hết cho 7

    _HT_

2)  1+2+3+...+n=1275

Ta thấy dãy số trên là dãy số cách đều nên có khoảng cách là 1 đơn vị 

=> Dãy số trên có n số hạng

Tổng của dãy số trên là :   (n+1).n:2 = 1275

                                          (n+1).n= 1275.2=2550

Mà n và n+1 là 2 số tự nhiên liên tiếp => (n+1).n = 51.50

=> n=50 ( vì n< n+1)

  Vậy n=50

_HT_

ko bt lm

Làm mẫu câu b)

b) n là số tự nhiên nên n có 1 trong 2 dạng 2k hoặc 2k + 1

TH1: n = 2k

\(\Rightarrow\) \(\left(2k+5\right)\left(2k+8\right)=2\left(k+4\right)\left(2k+5\right)⋮2\)

TH1: n = 2k +1

\(\Rightarrow\left(2k+1+5\right)\left(2k+1+8\right)=2\left(k+3\right)\left(2k+9\right)⋮2\)

a) Do (2n+5) là số lẻ,4n+2023 là số lẻ \(\Rightarrow\)(2n+5).(4n+2023) là số lẻ

\(\Rightarrow\)(2n+5).(4n+2023)  không chia hết cho 2

Vậy .................