điện trở tương đương của đoạn mạch gồm hai điện trở R1 và R2 nối tiếp nhau R1 = 5 ôm ,R2 = 3 ôm, điện trở tương đương bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(R_1ntR_2\)
Ta có : \(R_{tđ}=R_1+R_2\rightarrow R_2=R_{tđ}-R_1=9-3=6\left(\Omega\right)\)

a. Ta có: R2 = 3R1
Điện trở R1 là:
Rtđ = R1 + R2
Rtđ = R1 + 3R1
24 = 4R1
=> R1 = 24/4 = 6(ôm)
b) Vì R1 nt R2 nt R3 => Điện trở tương đương của mạch:
Rtđ = R1 + R2 + R3 = 29 + 15 + 27 = 71 (ôm)
c) Vì R1 // R2 // R3 => Điện trở tương đương của mạch:
\(\text{\dfrac{1}{Rtđ} = }\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{250}+\dfrac{1}{50}+\dfrac{1}{750}=\dfrac{19}{750}\)
=> Rtđ = \(\dfrac{750}{19}=39,47\) (ôm)

Tóm tắt :
Biết : \(R_1=3\Omega\) ; \(R_2=5\Omega\) ; \(R_3=7\Omega\)
\(U=6V\)
Tính : a. \(R_{tđ}=?\)
b. \(U_1=?\) ; \(U_2=?\) ; \(U_3=?\)
Giải
a. Vì \(R_2\) nt \(R_2\) nt \(R_3\) nên điện trở tương đương của đoạn mạch là :
\(R_{tđ}=R_1+R_2+R_3=3+5+7=15\Omega\)
b. CĐDĐ qua mạch chính là :
\(I=\dfrac{U}{R}=\dfrac{6}{15}=0,4A\)
Do \(R_1\) nt \(R_2\) nt \(R_3\) nên :
\(I=I_1=I_2=I_3=0,4A\)
HĐT giữa hai đầu mỗi điện trở là :
\(U_1=I_1.R_1=0,4.3=1,2V\)
\(U_2=I_2.R_2=0,4.5=2V\)
\(U_3=I_3.R_3=0,4.7=2,8V\)
Đáp số : a. \(R_{tđ}=15\Omega\)
b. \(U_1=1,2V\) ; \(U_2=2V\) ; \(U_3=2,8V\)

Điện trở tương đương là
\(R_{tđ}=R_1+R_2=6+3=9\left(\Omega\right)\)

ĐIện trở tương đương của đoạn mạch:
\(R_{tđ}=R_1+R_2=10+15=25\left(\Omega\right)\)

\(\Rightarrow R1ntR2ntR3nt....ntR2015\)
\(\Rightarrow Rtd=R1+R2+R3+..+R2015=1+2+3+...+2015\)
\(\Rightarrow Rtd=1+2+3+...+2015\)
\(\Rightarrow Rtd=2015+2014+2013+...+1\)
\(\Rightarrow2Rtd=2016+2016+...+2016\)(có 2015 số 2016)
\(\Rightarrow2Rtd=2015.2016\Rightarrow Rtd=\text{2031120}\left(\Omega\right)\)

a) Do \(R_1ntR_2\)
\(\Rightarrow R_{td}=R_1+R_2=5+15=20\Omega\)
b) \(I=\dfrac{U}{R_{td}}=\dfrac{12}{20}=0,6A\)
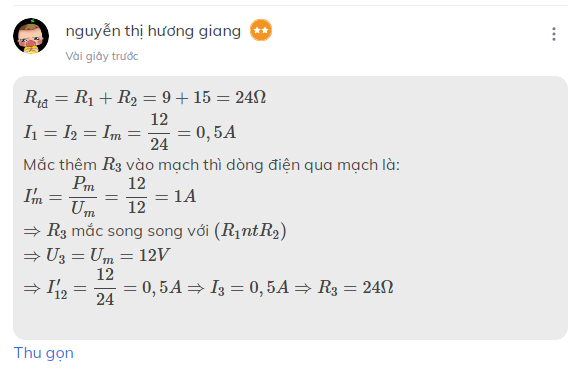
Mạch có \(R_1ntR_2\)
Điện trở tương đương: \(R_{tđ}=R_1+R_2=5+3=8\Omega\)