Bài 17: ( 2.5 điểm) Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B e (O), C € (O'). Tiếp tuyến chung trong tại A cất tiếp tuyển chung ngoài BC ở I a) Chứng minh rằng BAC = 90°. b) Tính độ dài BC biết OA = 9cm, O'A = 4cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 10 2019
a) Ta có:
IA = IB = IC
Tam giác BAC có AI là trung tuyến và AI = BC/2
⇒ Tam giác BAC vuông tại A hay ∠BAC = 90 0
CM
18 tháng 12 2019
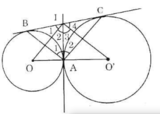
Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
tam giác ABC có đường trung tuyến AI = 1/2 BC nên là tam giác vuông
vậy B A C ^ = 90 o
CM
23 tháng 4 2017
a, Chứng minh được B A C ^ = 90 0 kết hợp B A D ^ = C A E ^ = 90 0 => ĐPCM
b, Chứng minh ∆BAD:∆EAC => AD.AE=AB.AC(đpcm)
c, Chứng minh tứ giác OIO’K là hình chữ nhật
Đường tròn ngoại tiếp ∆OKO’ chính là đường tròn ngoại tiếp hình chữ nhật ,có đường kính là IK mà IK ⊥ BC tại I
CM
6 tháng 1 2018
Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
O I O ' ^ = O I A ^ + O ' I A ^ = 1 2 A I B ^ + 1 2 A I C ^ = 1 2 A I B ^ + A I C ^
Vậy O I O ' ^ = 90 o
CM
16 tháng 10 2017
c) Xét tam giác OIO' vuông tại I, IA là đường cao có:
IA 2 = O'A.OA = 4.9 = 36 ⇒ IA = 6 cm
Lại có: BC = 2 AI ⇒ BC = 12 (cm)
CM
1 tháng 10 2019
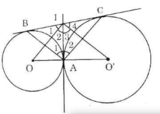
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
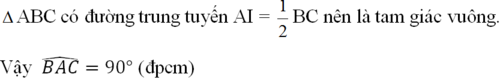
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
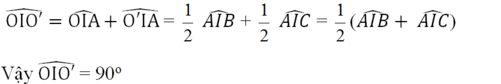
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
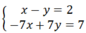
a.
Do IA và IB là tiếp tuyến của (O), theo t/c hai tiếp tuyến cắt nhau ta có: \(IA=IB\)
Tương tự, IA và IC là tiếp tuyến của (O') \(\Rightarrow IA=IC\)
\(\Rightarrow IA=IB=IC=\dfrac{1}{2}BC\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow\widehat{BAC}=90^0\)
b.
Theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{OIB}=\widehat{OIA}=\dfrac{1}{2}\widehat{BIA}\\\widehat{O'IC}=\widehat{O'IA}=\dfrac{1}{2}\widehat{CIA}\end{matrix}\right.\)
\(\Rightarrow\widehat{OIA}+\widehat{O'IA}=\dfrac{1}{2}\left(\widehat{BIA}+\widehat{CIA}\right)\)
\(\Rightarrow\widehat{OIO'}=\dfrac{1}{2}.\widehat{BIC}=\dfrac{1}{2}.180^0=90^0\)
\(\Rightarrow\Delta OIO'\) vuông tại O
Do IA là tiếp tuyến chung tại điểm tiếp xúc ngoài của 2 đường tròn \(\Rightarrow IA\perp O'O\)
Áp dụng hệ thức lượng trong tam giác vuông OIO' với đường cao IA:
\(IA^2=OA.O'A=36\Rightarrow IA=6\left(cm\right)\)
\(\Rightarrow BC=2IA=12\left(cm\right)\)