giúp vs ạaa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C



a) \(A=\left(x+5\right)^2-\left(x+3\right)^2\)
\(=\left[\left(x+5\right)-\left(x+3\right)\right]\left[\left(x+5\right)+\left(x+3\right)\right]\)
\(=\left(x+5-x-3\right)\left(x+5+x+3\right)\)
\(=2\left(2x+8\right)\)
\(=4x+16\)
b) \(B=\left(4x+1\right)^2-\left(2x+1\right)^2\)
\(=\left[\left(4x+1\right)-\left(2x+1\right)\right]\left[\left(4x+1\right)+\left(2x+1\right)\right]\)
\(=\left(4x+1-2x-1\right)\left(4x+1+2x+1\right)\)
\(=2x\left(6x+2\right)\)
\(=12x^2+4x\)
c) \(C=\left(3-4x\right)^2-\left(2x-1\right)\left(8x-9\right)\)
\(=9-24x+16x^2-16x^2+18x+8x-9\)
\(=\left(16x^2-16x^2\right)+\left(-24x+18x+8x\right)+\left(9-9\right)\)
\(=2x\)
d) \(D=\left(4+2x^2\right)-\left(1-4x\right)\left(4-x\right)\)
\(=4+2x^2-4+x+16x-4x^2\)
\(=\left(2x^2-4x^2\right)+\left(x+16x\right)+\left(4-4\right)\)
\(=-2x^2+17x\)
e) \(E=\left(2-3x\right)^2-2\left(2-3x\right)\left(3x+5\right)+\left(3x+5\right)^2\)
\(=\left(2-3x+3x+5\right)^2\)
\(=7^2\)
\(=49\)




Bài 2:
a: 2/3+1/2-1/6=4/6+3/6-1/6=3/6+3/6=1
b: \(=\dfrac{12}{24}\cdot\dfrac{23}{46}\cdot\dfrac{1}{2}=\dfrac{1}{4}\cdot\dfrac{1}{2}=\dfrac{1}{8}\)
c: =1/6x1/3=1/18
d: \(=\dfrac{48}{24}\cdot23=46\)

 giúp em vs ạaa
giúp em vs ạaa

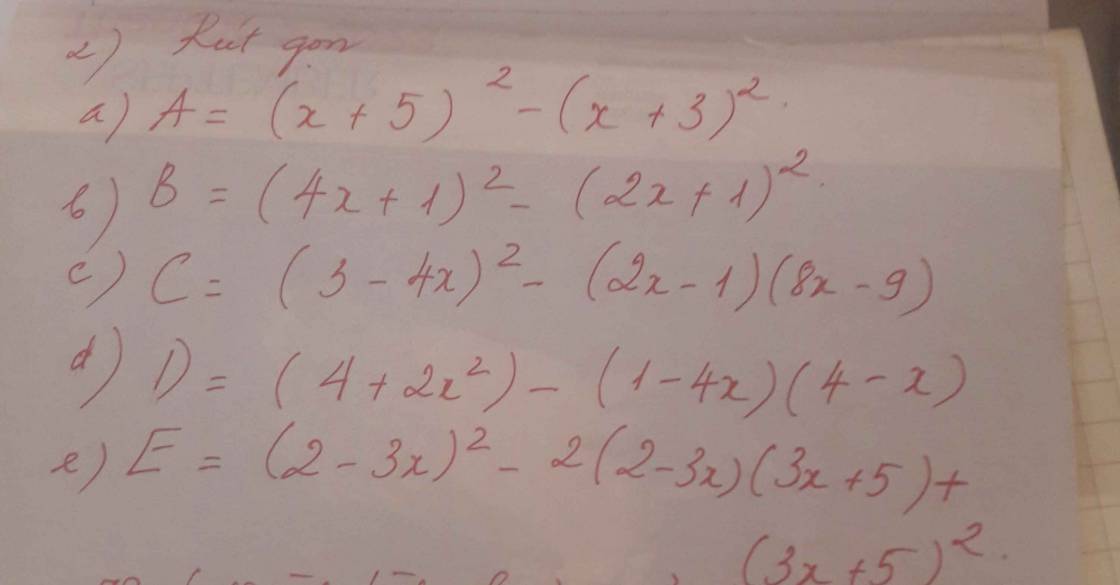
 giúp e vs ạaa
giúp e vs ạaa

 giúp em bàu 2 vs ạaa
giúp em bàu 2 vs ạaa
Bài 1:
\(A=3+3^2+...+3^{100}\)
=>\(3\cdot A=3^2+3^3+...+3^{101}\)
=>\(3A-A=3^2+3^3+...+3^{101}-3-3^2-...-3^{100}\)
=>\(2A=3^{101}-3\)
=>\(2A+3=3^{101}\)
mà \(2A+3=3^n\)
nên n=101
Bài 2:
a: \(M=3+3^2+3^3+3^4+...+3^{100}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{99}+3^{100}\right)\)
\(=\left(3+3^2\right)+3^2\left(3+3^2\right)+...+3^{98}\left(3+3^2\right)\)
\(=12\left(1+3^2+...+3^{98}\right)⋮12\)
=>\(M=4\cdot3\cdot\left(1+3^2+...+3^{98}\right)⋮4\)
b: \(M=3+3^2+...+3^{100}\)
=>\(3M=3^2+3^3+...+3^{101}\)
=>\(3M-M=3^2+3^3+...+3^{101}-3-3^2-...-3^{100}\)
=>\(2M=3^{101}-3\)
=>\(2M+3=3^{101}\)
=>n=101