 quy đồng chi tiết ạ e mới học nên làm từng bước ạ
quy đồng chi tiết ạ e mới học nên làm từng bước ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)

a: AB//CD
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(KA\cdot KD=KB\cdot KC\)
b: 

b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)

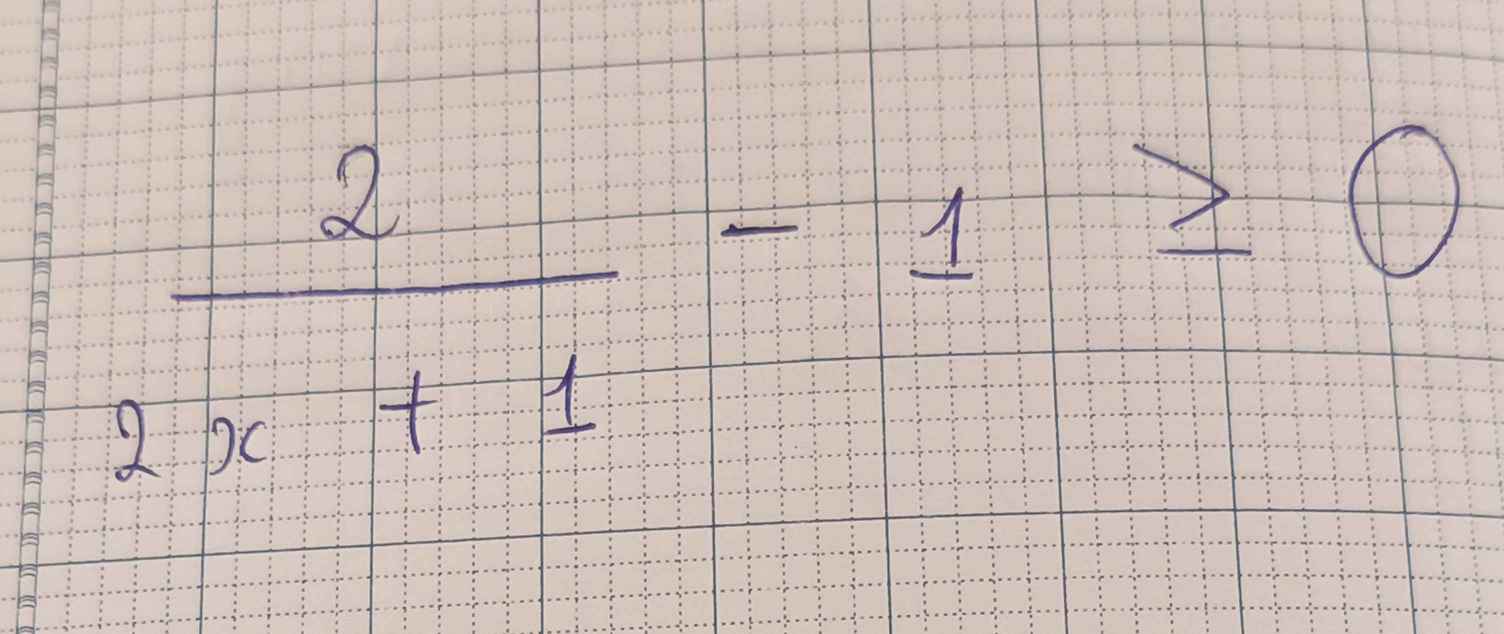
\(\dfrac{2}{2x+1}-1\ge0\Leftrightarrow\dfrac{2}{2x+1}-\dfrac{2x+1}{2x+1}\ge0\)
\(\Leftrightarrow\dfrac{2-\left(2x+1\right)}{2x+1}\ge0\)
\(\Leftrightarrow\dfrac{1-2x}{2x+1}\ge0\)
\(\Rightarrow-\dfrac{1}{2}< x\le\dfrac{1}{2}\)
Câu trả lời của cô rất hay cô ạ
Em rất cảm ơn cô vì câu trả lời này

a: \(Q=\dfrac{2x^2-4x+x-3-6}{\left(x-3\right)\left(x-2\right)}\cdot\dfrac{x-2}{x^2+1}=\dfrac{2x^2-3x-9}{x-3}\cdot\dfrac{1}{x^2+1}\)
\(=\dfrac{2x^2-6x+3x-9}{x-3}\cdot\dfrac{1}{x^2+1}=\dfrac{2x+3}{x^2+1}\)
b: Để Q>0 thì 2x+3>0
hay x>-3/2

\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)

a) Để phương trình có nghiệm thì: m2≠0 =>m≠0
b) Vì phương trình có nghiệm bằng -2m
=>-(m+2)2m-m2=0 ⇔-2m2-4m-m2=0 ⇔-3m2-4m=0 ⇔-m(3m+4)=0
⇔m=0 hay m=\(\dfrac{-4}{3}\)mà m phải khác 0 nên m=\(\dfrac{-4}{3}\).
c) -(m+2)x-m2=0 ⇔x=\(\dfrac{m^2}{m+2}\)>0 ⇔m+2>0 ⇔m>-2.
d) -(m+2)x-m2=0 ⇔x=\(\dfrac{m^2}{m+2}\).
Để x nguyên thì m2 ⋮ m+2.
⇔ m2-4+4 ⋮ m+2
⇔ 4 ⋮ m+2
⇔ m∈{-1;-3;0;-4;2;-6} mà m khác 0 nên m∈{-1;-3;-4;2;-6}


a: Xét ΔKAB và ΔKCD có
\(\widehat{KAB}=\widehat{KCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AKB}=\widehat{CKD}\)(hai góc đối đỉnh)
Do đó: ΔKAB đồng dạng với ΔKCD
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(KA\cdot KD=KB\cdot KC\)
b: Ta có: \(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(\dfrac{KC}{KA}=\dfrac{KD}{KB}\)
=>\(\dfrac{KC}{KA}+1=\dfrac{KD}{KB}+1\)
=>\(\dfrac{KC+KA}{KA}=\dfrac{KD+KB}{KB}\)
=>\(\dfrac{AC}{KA}=\dfrac{BD}{KB}\)
=>\(\dfrac{AK}{AC}=\dfrac{BK}{BD}\left(1\right)\)
Xét ΔADC có IK//DC
nên \(\dfrac{AK}{AC}=\dfrac{IK}{DC}\left(2\right)\)
Xét ΔBDC có KQ//DC
nên \(\dfrac{KQ}{DC}=\dfrac{BK}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra IK=KQ
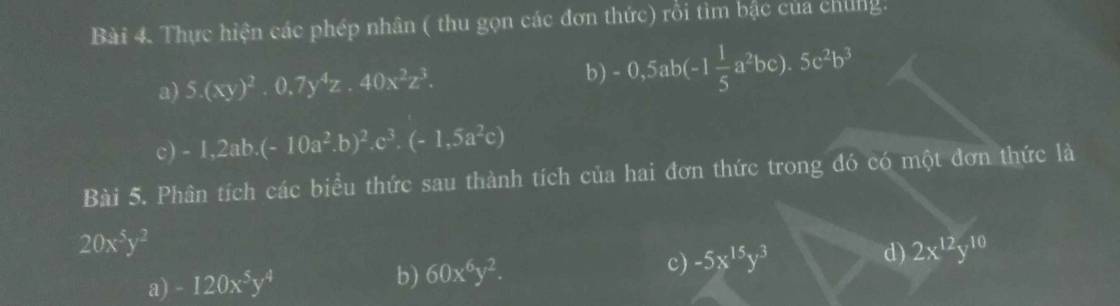

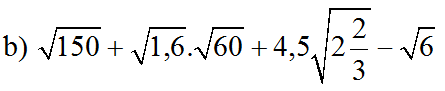
 ạ vì mình ko hiểu ạ
ạ vì mình ko hiểu ạ
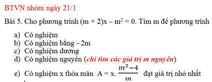
 giải chi tiết từng bước giúp mình ạ
giải chi tiết từng bước giúp mình ạ
Ta có:
\(3x-3=3\left(x-1\right)\)
\(4-4x=-4\left(x-1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
\(\Rightarrow\) MTC là \(3.\left(-4\right).\left(x-1\right)\left(x+1\right)=-12\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\dfrac{11x}{3x-3}=\dfrac{11x}{3\left(x-1\right)}=\dfrac{11x.\left(-4\right).\left(x+1\right)}{3\left(x-1\right).\left(-4\right)\left(x+1\right)}=\dfrac{-44x\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{5}{4-4x}=\dfrac{5}{-4\left(x-1\right)}=\dfrac{5.3\left(x+1\right)}{-4\left(x-1\right).3\left(x+1\right)}=\dfrac{15\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{2x}{x^2-1}=\dfrac{2x}{\left(x-1\right)\left(x+1\right)}=\dfrac{2x.\left(-12\right)}{-12\left(x-1\right)\left(x+1\right)}=\dfrac{-24x}{-12\left(x-1\right)\left(x+1\right)}\)