vẽ đồ thị của hàm số sau
a) \(y=log2x\)
b) \(y=log_{\dfrac{1}{4}}x\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Bảng giá trị:
| x | 1 | 2 | 3 |
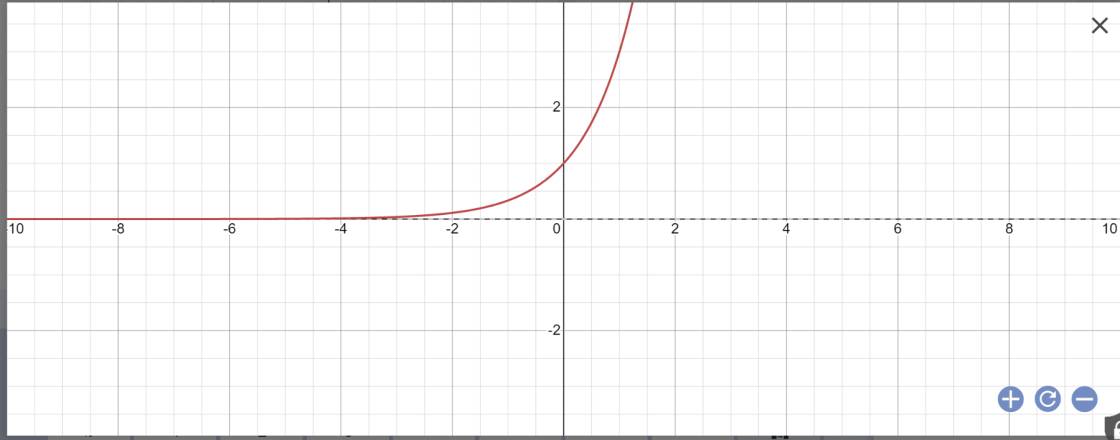
| \(y=3^x\) | 3 | 9 | 27 |
Vẽ đồ thị:
b: Bảng giá trị:
| x | 2 | 3 | 4 |
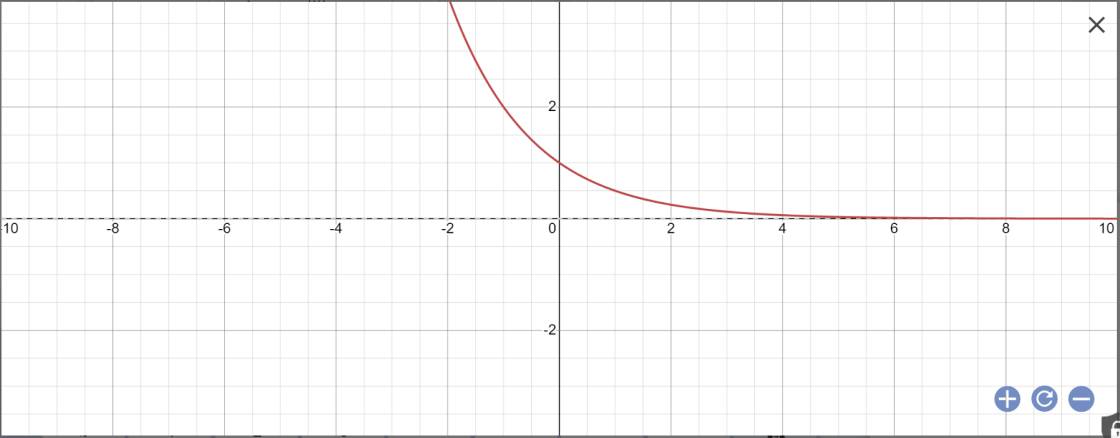
| \(y=\left(\dfrac{1}{2}\right)^x\) | 1/4 | 1/8 | 1/16 |
vẽ đồ thị:

a: \(\lim\limits_{x\rightarrow3}\dfrac{x+3}{x^2-9}=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow3}x+3=3+3=6\\\lim\limits_{x\rightarrow3}x^2-9=0\end{matrix}\right.\)
=>x=3 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{x^2-9}\)
\(\lim\limits_{x\rightarrow-3}\dfrac{x+3}{x^2-9}=\lim\limits_{x\rightarrow-3}\dfrac{1}{x-3}=\dfrac{1}{-3-3}=-\dfrac{1}{6}\)
=>x=-3 không là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{x^2-9}\)
b: \(\lim\limits_{x\rightarrow5}\dfrac{x-5}{x^2-25}=\lim\limits_{x\rightarrow5}\dfrac{1}{x+5}=\dfrac{1}{5+5}=\dfrac{1}{10}\)
=>x=5 không là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-5}{x^2-25}\)
\(\lim\limits_{x\rightarrow-5}\dfrac{x-5}{x^2-25}=-\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-5}x-5=-5-5=-10< 0\\\lim\limits_{x\rightarrow-5}x^2-25=0\end{matrix}\right.\)
=>x=-5 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-5}{x^2-25}\)
c: \(\lim\limits_{x\rightarrow1}\dfrac{x^2-4x+3}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{x-3}{x+1}=\dfrac{1-3}{1+1}=\dfrac{-2}{2}=-1\)
=>x=1 không là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x^2-4x+3}{x^2-1}\)
\(\lim\limits_{x\rightarrow-1}\dfrac{x^2-4x+3}{x^2-1}=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-1}x^2-4x+3=\left(-1\right)^2-4\cdot\left(-1\right)+3=8>0\\\lim\limits_{x\rightarrow-1}x^2-1=0\end{matrix}\right.\)
=>x=-1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x^2-4x+3}{x^2-1}\)
d: \(\lim\limits_{x\rightarrow3}\dfrac{x^2-3x-4}{x^2-2x-3}=-\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow3}x^2-3x-4=3^2-3\cdot3-4=-4< 0\\\lim\limits_{x\rightarrow3}x^2-2x-3=0\end{matrix}\right.\)
=>x=3 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x^2-3x-4}{x^2-2x-3}\)
\(\lim\limits_{x\rightarrow-1}\dfrac{x^2-3x-4}{x^2-2x-3}=\lim\limits_{x\rightarrow-1}\dfrac{\left(x-4\right)\left(x+1\right)}{\left(x-3\right)\left(x+1\right)}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{x-4}{x-3}=\dfrac{-1-4}{-1-3}=\dfrac{5}{4}\)
=>x=-1 không là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x^2-3x-4}{x^2-2x-3}\)

a: \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{9+\dfrac{1}{x}}+1}{2+\dfrac{5}{x}}=\dfrac{\sqrt{9}+1}{2}=\dfrac{3+1}{2}=2\)
=>Đường thẳng y=2 là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{9+\dfrac{1}{x}}+1}{2+\dfrac{5}{x}}=\dfrac{-3+1}{2}=\dfrac{-2}{2}=-1\)
=>Đường thẳng y=-1 là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
b: \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{2+\dfrac{1}{x^2}}-1}{1+\dfrac{2}{x}}=\dfrac{\sqrt{2}-1}{1}=\sqrt{2}-1\)
=>Đường thẳng \(y=\sqrt{2}-1\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{2+\dfrac{1}{x^2}}-1}{1+\dfrac{2}{x}}=\dfrac{-\sqrt{2}-1}{1}=-\sqrt{2}-1\)
=>Đường thẳng \(y=-\sqrt{2}-1\) là một tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)

a) Đồ thị của hàm số \(y=\log_3\left(x-1\right)\) nhận được từ đồ thị của hàm số \(y=\log_3x\) bằng cách tịnh tiến song song với trục hoành sang bên phải 1 đơn vị
b) Đồ thị của hàm số \(y=\log_{\dfrac{1}{3}}\left(x+1\right)\) nhận được từ đồ thị của hàm số \(y=\log_{\dfrac{1}{3}}x\) bằng cách tịnh tiến song song với trục hoành sang bên trái 1 đơn vị
c) Đồ thị của hàm số \(y=1+\log_3x\) nhận được từ đồ thị của hàm số \(y=\log_3x\) bằng cách tịnh tiến song song với trục tung lên trên 1 đơn vị

a: \(\lim\limits_{x\rightarrow2^+}\dfrac{\sqrt{x-2}+1}{x^2-3x+2}=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow2^+}\sqrt{x-2}+1=\sqrt{2-2}+1=1>0\\\lim\limits_{x\rightarrow2^+}x^2-3x+2=\lim\limits_{x\rightarrow2^+}\left(x-1\right)\left(x-2\right)=0\end{matrix}\right.\)
=>x=2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{\sqrt{x-2}+1}{x^2-3x+2}\)
b: \(\lim\limits_{x\rightarrow-5^+}\dfrac{\sqrt{5+x}-1}{x^2+4x}=\dfrac{\sqrt{5-5}-1}{\left(-5\right)^2+4\cdot\left(-5\right)}=\dfrac{-1}{25-20}=\dfrac{-1}{5}\)
=>x=-5 không là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{\sqrt{5+x}-1}{x^2+4x}\)
\(\lim\limits_{x\rightarrow\left(-4\right)^+}\dfrac{\sqrt{5+x}-1}{x^2+4x}\)
\(=\lim\limits_{x\rightarrow\left(-4\right)^+}\dfrac{5+x-1}{\left(\sqrt{5+x}+1\right)\left(x^2+4x\right)}=\lim\limits_{x\rightarrow\left(-4\right)^+}\dfrac{x+4}{\left(\sqrt{5+x}+1\right)\cdot x\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow\left(-4\right)^+}\dfrac{1}{x\left(\sqrt{5+x}+1\right)}=\dfrac{1}{\left(-4\right)\cdot\left(\sqrt{5-4}+1\right)}=\dfrac{1}{-8}=-\dfrac{1}{8}\)
=>x=-4 không là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{\sqrt{5+x}-1}{x^2+4x}\)
\(\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{5+x}-1}{x^2+4x}=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow0^+}\sqrt{5+x}-1=\sqrt{5+0}-1=\sqrt{5}-1>0\\\lim\limits_{x\rightarrow0^+}x^2+4x=0\end{matrix}\right.\)
=>Đường thẳng x=0 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{\sqrt{5+x}-1}{x^2+4x}\)
c: \(\lim\limits_{x\rightarrow0^+}\dfrac{5x+1-\sqrt{x+1}}{x^2+2x}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{5x+1-x^2-2x-1}{5x+1+\sqrt{x+1}}}{x\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{-x^2+3x}{\left(5x+1+\sqrt{x+1}\right)\cdot x\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{-x\left(x-3\right)}{x\left(x+2\right)\left(5x+1+\sqrt{x+1}\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{-x+3}{\left(x+2\right)\left(5x+1+\sqrt{x+1}\right)}=\dfrac{-0+3}{\left(0+2\right)\left(5\cdot0+1+\sqrt{0+1}\right)}\)
\(=\dfrac{3}{2\cdot\left(6+1\right)}=\dfrac{3}{14}\)
=>x=0 không là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{5x+1-\sqrt{x+1}}{x^2+2x}\)
\(\lim\limits_{x\rightarrow\left(-2\right)^+}\dfrac{5x+1-\sqrt{x+1}}{x^2+2x}\) không có giá trị vì khi x=-2 thì căn x+1 vô giá trị
=>Đồ thị hàm số \(y=\dfrac{5x+1-\sqrt{x+1}}{x^2+2x}\) không có tiệm cận đứng
d: \(\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{4x^2-1}+3x^2+2}{x^2-x}\) không có giá trị vì khi x=0 thì \(\sqrt{4x^2-1}\) không có giá trị
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{4x^2-1}+3x^2+2}{x^2-x}\)
\(=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow1^+}\sqrt{4x^2-1}+3x^2+2=\sqrt{4-1}+3\cdot1^2+2=5+\sqrt{3}>0\\\lim\limits_{x\rightarrow1^+}x^2-x=0\end{matrix}\right.\)
=>x=1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{\sqrt{4x^2-1}+3x^2+2}{x^2-x}\)

a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)


a, Hoành độ giao điểm tm pt
\(x^2-\dfrac{1}{2}x=0\Leftrightarrow x\left(x-\dfrac{1}{2}\right)=0\Leftrightarrow x=0;x=\dfrac{1}{2}\)
Với x = 0 => y = 0
Với x = 1/2 => y = 1/4
Vậy (P) cắt (d) tại O(0;0) ; A(1/2;1/4)
a: Bảng giá trị:
Vẽ đồ thị:
b: bảng giá trị:
Vẽ đồ thị: