Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

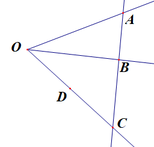
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC

a) Xét ▲OAD và ▲OBC có :
OA = OB ( gt )
góc COD chung
OC = OD ( gt )
=> ▲OAD = ▲OBC ( c-g-c )
=> đpcm
b) Gọi giao điểm của BC và AD là M
Vì ▲OAD = ▲OBC ( c/m trên )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Xét ▲ACM có góc MAC + góc ACM + góc CMA = 1800
Xét ▲BMD có góc BMD + góc MDB + góc DBM = 1800
Mà góc OCB = góc ODA ( c/m trên ) và góc CMA = góc BMD ( đối đỉnh )
=> góc CAM = góc MBD ( đpcm )

* Trường hợp 1: O nằm giữa A, B:
- C nằm giữa B, D: OA và OB, CD và CB
- B nằm giữa C, D: OA và OB, BC và BD
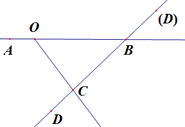
* Trường hợp 2: A nằm giữa O, B:
- C nằm giữa B, D: AO và AB, CD và CB
- B nằm giữa C, D: AO và AB, BC và BD
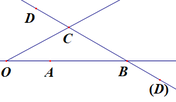
* Trường hợp 3: B nằm giữa A, O:
- C nằm giữa B, D: BA và BO, CD và CB
- B nằm giữa C, D: BA và BO, BC và BD