Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADBK có
M là trung điểm chung của AB và DK
=>ADBK là hình bình hành
=>AK=DB
mà DB=AC(ABCD là hình chữ nhật)
nên AK=AC
=>ΔAKC cân tại A
b: Xét ΔIAM có IE là phân giác
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IA}\)
mà IA=IK
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IK}\)
Xét ΔIMK có IF là phân giác
nên \(\dfrac{IM}{IK}=\dfrac{MF}{FK}\)
=>\(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
Xét ΔMAK có \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
nên EF//AK
Ta có: EF//AK
AK//BD(AKBD là hình bình hành)
Do đó: EF//BD

a.
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)

1: Xét tứ giác AMND có
\(\widehat{ADN}=\widehat{DAM}=\widehat{MND}=90^0\)
Do đó: AMND là hình chữ nhật
2: Xét tứ giác AKBD có
M là trung điểm của đường chéo KD
M là trung điểm của đường chéo AB
Do đó: AKBD là hình bình hành
Trả lời:
1: Xét tứ giác AMND có
ˆADN=ˆDAM=ˆMND=900ADN^=DAM^=MND^=900
Do đó: AMND là hình chữ nhật
2: Xét tứ giác AKBD có
M là trung điểm của đường chéo KD
M là trung điểm của đường chéo AB
Do đó: AKBD là hình bình hành
Chúc bạn học tốt nhé.

Ta có: AM=MB=AB/2 ( M là trung điểm AB)
DN=NC=DC/2 (N là trung điểm DC)
Mà: AB=AC (ABCD LÀ HBH)
=> AM=MB=DN=NC
Xét tứ giác AMCN:
AM=NC (cmt)
AM//NC (AB//CD)
Vậy AMCN là hình bình hành
b.
Xét tứ giác AMND:
AM=ND (cmt)
AM//ND (AB//CD)
Vậy AMDN là hình bình hành
C. hình như bạn chép sai đề rồi: TK??

a: Sửa đề; B đối xứng D qua N
Xét tứ giac ABCD có
N là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AB//CD
b: Xét tứ giá AMBP có
I là trung điểm chung của AB và MP
AB vuông góc với MP
Do đó: AMBP là hình thoi

a: Xét tứ giác AMND có
\(\widehat{MAD}=\widehat{ADN}=\widehat{MND}=90^0\)
nên AMND là hình chữ nhật

a) xét từ giác ADMN có:
\(\widehat{MAD}=90^o\) (ABCD là hình chữ nhật)
\(\widehat{ADN}=90^o\) (ABCD là hình chữ nhật)
\(\widehat{DNM}=90^o\) (giả thiết)
⇒ từ giác ADMN là hình chữ nhật
b) xét từ giác ADBK có:
MA = MB (M là trung điểm AB)
MD = MK (M là trung điểm của DK)
⇒ từ giác ADBK là hình bình hành
Ta có : BD = AK (vì tứ giác ADBK là hình bình hành) (1)
Lại có: AC = BD (vì ABCD là hình chữ nhật) (2)
Từ (1) và (2) ⇒ AK = AC
⇒ ΔACK là Δ cân tại A

a) Xét tứ giác AMND có
AM//ND
\(AM=ND\left(\dfrac{1}{2}AB=\dfrac{1}{2}CD\right)\)
Do đó: AMND là hình bình hành
Suy ra: AD=MN
b) Xét tứ giác BCNM có
BM//CN
\(BM=CN\left(\dfrac{1}{2}AB=\dfrac{1}{2}CD\right)\)
Do đó: BCNM là hình bình hành
Xét tứ giác AMCN có
AM//CN
\(AM=CN\left(\dfrac{1}{2}AB=\dfrac{1}{2}CD\right)\)
Do đó: AMCN là hình bình hành
Suy ra: AN//CM
hay EN//MF
Xét tứ giác BMDN có
BM//DN
\(BM=DN\left(\dfrac{1}{2}AB=\dfrac{1}{2}DC\right)\)
Do đó: BMDN là hình bình hành
Suy ra: BN//MD
hay NF//ME
Xét tứ giác MENF có
ME//NF(cmt)
MF//NE(cmt)
Do đó: MENF là hình bình hành

(tự vẽ hình nha)
a,Ta có AM+MB=AB
NC+CD=DC
mà AB=CD(ABCD là HCN)
AM = NC (gt)
=> MB=DN (1)
Ta lại có AB//DC nên MB//DN (2)
Từ (1) và (2) => MBND là HBH
b,ta có : P là trung điểm AB
K là trung điểm AH
=>PK là đường trung bình tam giác AHB
=PK//BH (*)
mà BH//DM (MBND là HBH) (**)
từ (*) và (**) => PK//DM (ĐPCM)
c,do PK là đường trung bình
=>PK=1/2BH
=>PK = BH/2 = 6/2 =3cm
P là trung điểm AB
=> AP = 1/2AB = AB/2 = 10/2 = 5cm
ta có BH⊥AC mà BH//PK => AC⊥PK
=>△APK vuông tại K
S△APK là = 1/2AK.KP = 1/2.5.3 = 7,5
phần d mình chưa nghĩ ra
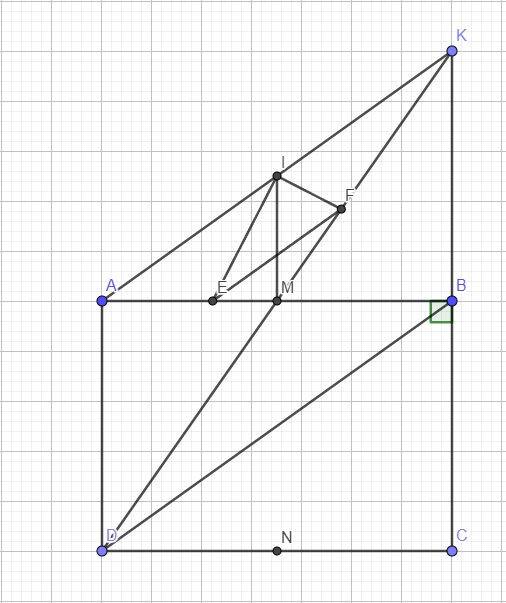
a: Sửa MN\(\perp\)CD tại N
Xét tứ giác AMND có
\(\widehat{MND}=\widehat{MAD}=\widehat{ADN}=90^0\)
=>AMND là hình chữ nhật
b: Xét tứ giác ADBK có
M là trung điểm chung của AB và DK
=>ADBK là hình bình hành
=>AK=BD
mà BD=AC(ABCD là hình chữ nhật)
nên AK=AC
=>ΔAKC cân tại A
c: Xét ΔMAI có IE là phân giác
nên \(\dfrac{ME}{EA}=\dfrac{MI}{IA}=\dfrac{MI}{IK}\left(1\right)\)
Xét ΔIMK có IF là phân giác
nên \(\dfrac{MF}{FK}=\dfrac{IM}{IK}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
Xét ΔMAK có \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
nên EF//AK
mà AK//BD(AKBD là hình bình hành)
nên EF//BD