a) Em có thể dùng 27 khối lập phương nhỏ để ghép thành khối lập phương lớn như sau:

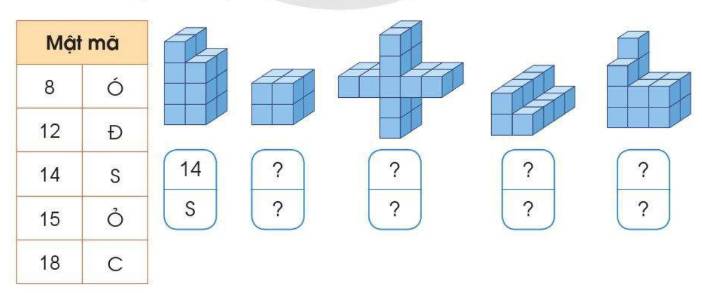
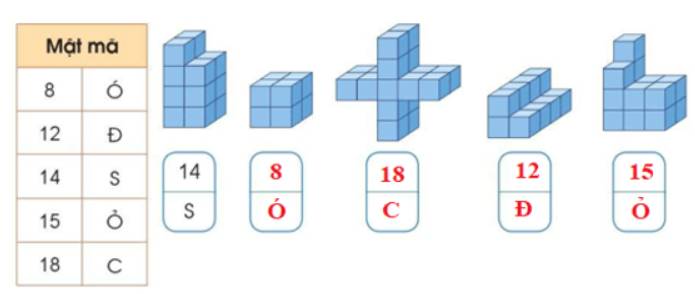
b) Em đếm các khối lập phương nhỏ trong mỗi hình và điền được như sau:

Ô chữ: SÓC ĐỎ

không thể xếp thành một hình lập phương mới được

ko thể xếp được

8 + 27 = 35 khối lập phương có cạnh là 1cm . Mũ 3 của một số không thể là 35.

Không thể tạo thành một hình lập phương mới được.
Giải thích: Vì khối lập phương được xếp từ 27 khối lập phương nhỏ có chiều dài cạnh là 1cm sẽ có số ô vuông trong một mặt là 3x3=9(nhẩm tính thôi) mỗi mặt của khối lập phương đó có 9 khối lập phương nhỏ cạnh 1cm. Vậy nếu cộng thêm 8 khối lập phuơng nhỏ cạnh 1cm nữa vào thì không tạo được một khối lập phương mới.

 S toàn phần của hình lập phương được tạo bởi 8 khối gỗ hình lập phương là:

          ( 1x1) x 4 x 8 = 32 cm vuông

S toàn phần của hình lập phương được tạo bởi 27 khối hình lâp phương nhỏ là:

           (1x1) x4 x 27 = 108 cm vuông 

tổng số S toàn phần của 2 hình là:

      108+32 =140

có thể nên mỗi mặt sẽ cần 140 : 4 = 35 khối

Các cậu giúp mình với.Mình đang cần gấp!!!!

HELP ME

Không thể tạo thành một hình lập phương mới được. 
Vì khối lập phương được xếp từ 27 khối lập phương nhỏ có chiều dài cạnh là 1cm sẽ có số ô vuông trong một mặt là 3x3=9, mỗi mặt của khối lập phương đó có 9 khối lập phương nhỏ cạnh 1cm. Vậy nếu cộng thêm 8 khối lập phuơng nhỏ cạnh 1cm nữa vào thì không tạo được một khối lập phương mới.

Không thể tạo thành một hình lập phương mới được. 
Vì khối lập phương được xếp từ 27 khối lập phương nhỏ có chiều dài cạnh là 1cm sẽ có số ô vuông trong một mặt là 3x3=9, mỗi mặt của khối lập phương đó có 9 khối lập phương nhỏ cạnh 1cm. Vậy nếu cộng thêm 8 khối lập phuơng nhỏ cạnh 1cm nữa vào thì không tạo được một khối lập phương mới.