Cho hình chóp S.ABCD có đáy là hình thang ABCD với AD//BC và AD = 2BC. Gọi M là điểm trên cạnh SD thỏa mãn SM = 1/3SD. Mặt phẳng (ABM) cắt cạnh SC tại N. Tính SN/ SC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
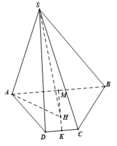
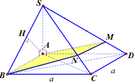
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) ![]()

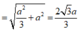
![]()
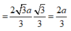
![]()
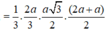
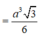

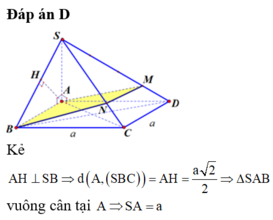
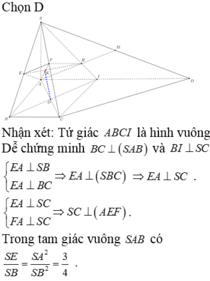
Đáp án D
Kẻ A H ⊥ S B ⇒ d A , S B C = A H = a 2 2 ⇒ Δ S A B vuông cân tại A ⇒ S A = a
⇒ V S . A B C D = 1 3 . S A . S A B C D = 1 3 . a . a 2 = a 3 3 .
Kẻ M N / / C D ⇒ S M S D = S N S C = 3 4
Ta có: V S . A B D = V S . B C D = 1 2 V S . A B C D
V S . A M N B V S . A B C D = V S . A B M + V S . B M N 2 V S . A B D = 1 2 V S . A B M V S . A B D + V S . B M N V S . A B D = 1 2 S M S D + S M S D . S N S C = 1 2 3 4 + 3 4 . 3 4 = 21 32 ⇒ V M N A B C D V S . A B C D = 11 32 V S . A B C D = 11 32 . a 3 3 = 11 a 3 96
Vậy
V M N A B C D = 11 32 V S . A B C D = 11 32 . a 3 3 = 11 a 3 96

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

Tham khảo hình vẽ:
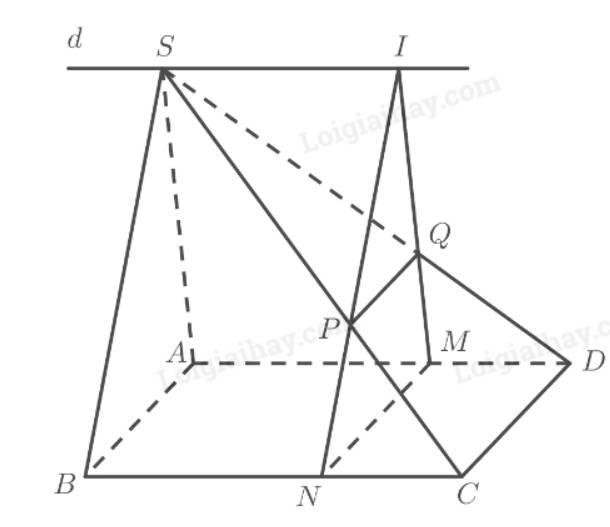
a) Ta có:
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {SC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\PQ = \left( \alpha \right) \cap \left( {SC{\rm{D}}} \right)\\MN\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel C{\rm{D}}\parallel PQ\).
\( \Rightarrow MNPQ\) là hình bình hành.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in MQ \Rightarrow I \in \left( {SA{\rm{D}}} \right)\\I \in NP \Rightarrow I \in \left( {SBC} \right)\end{array} \right\} \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\ \Rightarrow SI = \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel SI\).
Vậy \(I\) luôn luôn thuộc đường thẳng \(d\) đi qua \(S\) song song với \(AD\) và \(BC\) cố định khi \(M\) di động trên \(AD\).

Bài này ứng dụng 1 phần cách giải của bài này:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
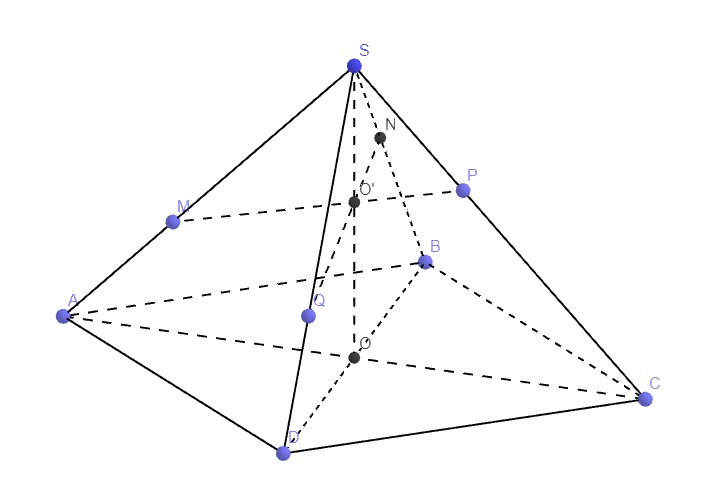
Gọi O' là giao điểm của SO và MP, tương tự như bài trên, ta có 3 đường thẳng SO, MP, NQ đồng quy tại O'
Đồng thời sử dụng diện tích tam giác, ta cũng chứng minh được:
\(3=\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{2SO}{SO'}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\)
Áp dụng BĐT Cô-si: \(3=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\ge2\sqrt{\dfrac{SB.SD}{SN.SQ}}\Rightarrow SN.SQ\ge\dfrac{4}{9}.SB.SD\)
Theo bổ đề về diện tích tam giác chứng minh ở đầu:
\(\dfrac{S_{SNQ}}{S_{SBD}}=\dfrac{SN.SQ}{SB.SD}\ge\dfrac{\dfrac{4}{9}SB.SD}{SB.SD}=\dfrac{4}{9}\)
\(\Rightarrow S_{SBD}\ge\dfrac{4}{9}.S_{SBD}=\dfrac{4}{9}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{9}\)


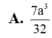
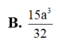
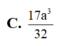
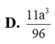
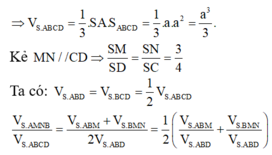
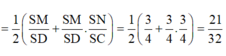
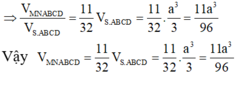


Vẫn dùng kĩ thuật cũ:
\(\overrightarrow{AD}-2\overrightarrow{BC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AS}+\overrightarrow{SD}-2\overrightarrow{BS}-2\overrightarrow{SC}=0\)
\(\Leftrightarrow\overrightarrow{SA}=2\overrightarrow{SB}-2\overrightarrow{SC}+\overrightarrow{SD}\) (1)
Đặt \(\overrightarrow{SC}=x.\overrightarrow{SN}\)
Giả thiết suy ra \(\overrightarrow{SD}=3\overrightarrow{SM}\)
Thế vào (1): \(\overrightarrow{SA}=2\overrightarrow{SB}-2x.\overrightarrow{SN}+3\overrightarrow{SM}\)
Do A, B, N, M đồng phẳng
\(\Rightarrow2-2x+3=1\)
\(\Rightarrow x=2\Rightarrow SC=2SN\Rightarrow SN=\dfrac{1}{2}SC\)