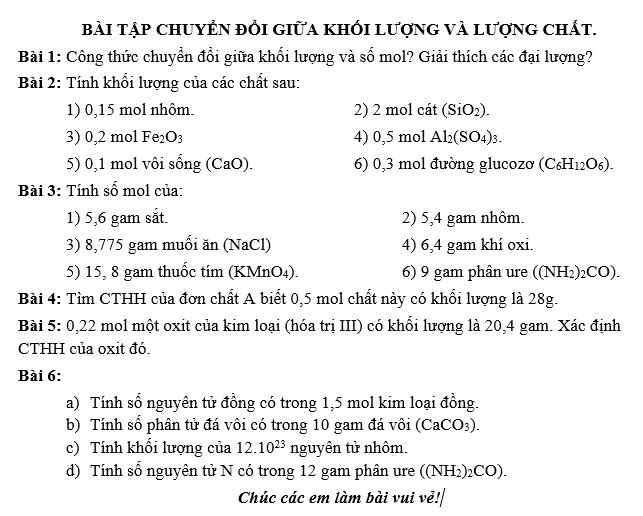
Bài 5:

Gọi kim loại đó là R thì CTHH oxit KL đó là \(R_2O_3\)

\(M_{R_2O_3}=\dfrac{20,4}{0,22}\approx102(g/mol)\\ \Rightarrow M_R=\dfrac{102-3.16}{2}=27(g/mol)\\ \text {Vậy R là nhôm (Al) và CTHH oxit là }Al_2O_3\)

Bài 6:

\(a,1,5.6.10^{-23}=9.10^{-23}(\text {nguyên tử Cu})\\ b,n_{CaCO_3}=\dfrac{10}{100}=0,1(mol)\\ \text {Số phân tử đá vôi là: }0,1.6.10^{-23}=0,6.10^{-23}\\ c,n_{Al}=\dfrac{12.10^{-23}}{6.10^{-23}}=2(mol)\\ \Rightarrow m_{Al}=2.27=54(g)\\ d,\%_N=\dfrac{14.2}{60}.100\%=\dfrac{140}{3}\%\\ \Rightarrow m_{N}=12.\dfrac{140}{3}\%=5,6(g)\\ \Rightarrow n_{N}=\dfrac{5,6}{14}=0,4(mol)\\ \text {Số nguyên tử N là: }0,4.6.10^{-23}=2,4.10^{-23}\)

 em cảm ơn ạ

giúp mình dzới ạ 

Khó thấy quá bạn ơi, bạn chụp lại đi

Lời giải:
a.

\(A=\left[\frac{1}{\sqrt{x}(\sqrt{x}+2)}-\frac{\sqrt{x}}{\sqrt{x}(\sqrt{x}+2)}\right]:\frac{1-\sqrt{x}}{(\sqrt{x}+2)^2}\)

\(=\frac{1-\sqrt{x}}{\sqrt{x}(\sqrt{x}+2)}.\frac{(\sqrt{x}+2)^2}{1-\sqrt{x}}=\frac{\sqrt{x}+2}{\sqrt{x}}\)

b.

$A=\frac{5}{2}\Leftrightarrow \frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{2}$

$\Leftrightarrow 1+\frac{2}{\sqrt{x}}=\frac{5}{2}$

$\Leftrightarrow \frac{2}{\sqrt{x}}=\frac{3}{2}$

$\Leftrightarrow \sqrt{x}=\frac{4}{3}$

$\Leftrightarrow x=\frac{16}{9}$ (thỏa đkxđ)

a) \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)

\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^0\\sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\Rightarrow\widehat{C}=37^0\end{matrix}\right.\)

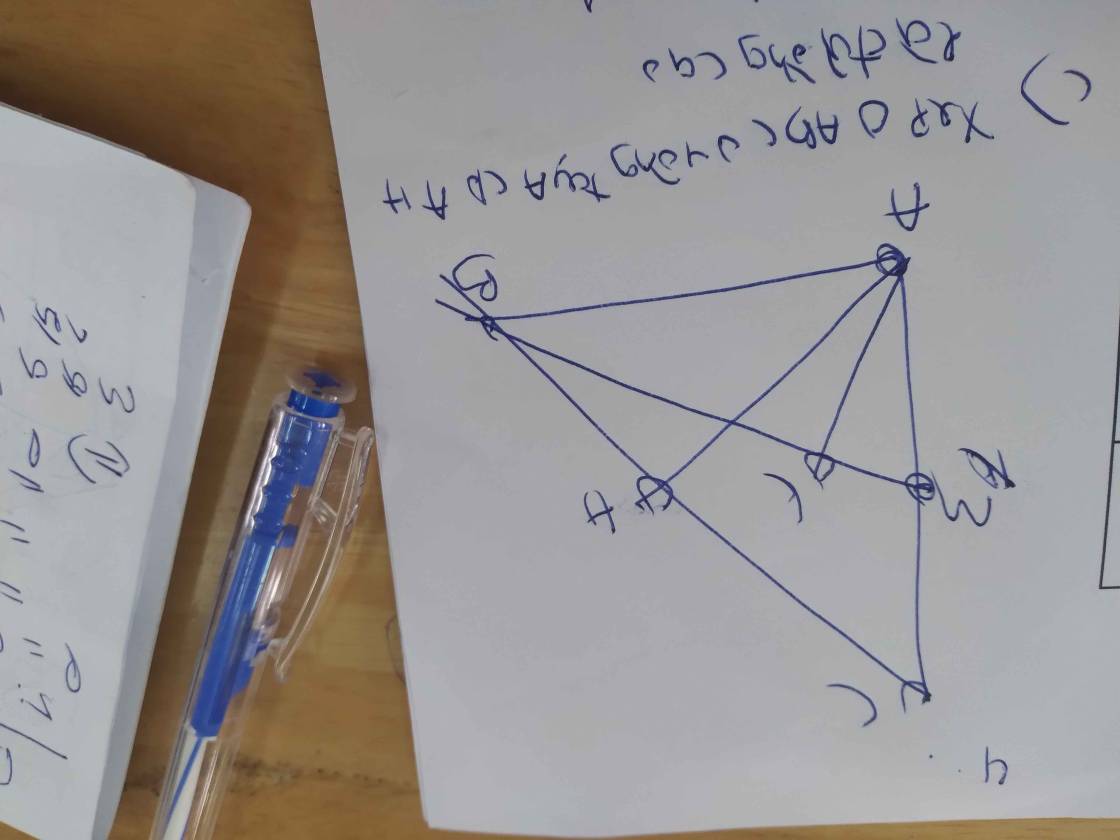
c) Ta có: \(\left\{{}\begin{matrix}AB=BD\\AC=DC\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)

=> BC là đường trung trực AD

\(\Rightarrow AD\perp BC\)

Áp dụng HTL trong tam giác BDC vuông tại D:

\(FB.FC=FD^2\Rightarrow4FB.FC=4FD^2=\left(2FD\right)^2=AD^2\)

Bài 5.

Cơ năng ban đầu:

\(W=\dfrac{1}{2}mv^2+mgz=0,5\cdot10\cdot120=600J\)

a)Cơ năng vật khi chạm đất: \(W'=0J\)

Vận tốc vật khi chạm đất:

\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot120}=20\sqrt{6}\)m/s

b)Cơ năng tại nơi \(W_t=3W_đ\):

\(W_1=W_đ+W_t=4W_đ=4\cdot\dfrac{1}{2}mv'^2=2\cdot0,5\cdot v'^2\left(J\right)\)

Bảo toàn cơ năng: \(W=W_1\)

\(\Rightarrow600=2\cdot0,5\cdot v'^2\Rightarrow v'=10\sqrt{6}\)m/s

c)Độ biến thiên động năng:

\(A_c=W_2-W_1=\dfrac{1}{2}m\left(v_1^2-v_2^2\right)\)

\(\Rightarrow-F_c\cdot s=\dfrac{1}{2}\cdot0,5\cdot\left(0^2-\left(20\sqrt{6}\right)^2\right)=-600\)

\(\Rightarrow-F_c=\dfrac{-600}{s}=\dfrac{-600}{0,3}=-2000N\)

\(\Rightarrow F_c=2000N\)

đăng từng câu 1 thôi

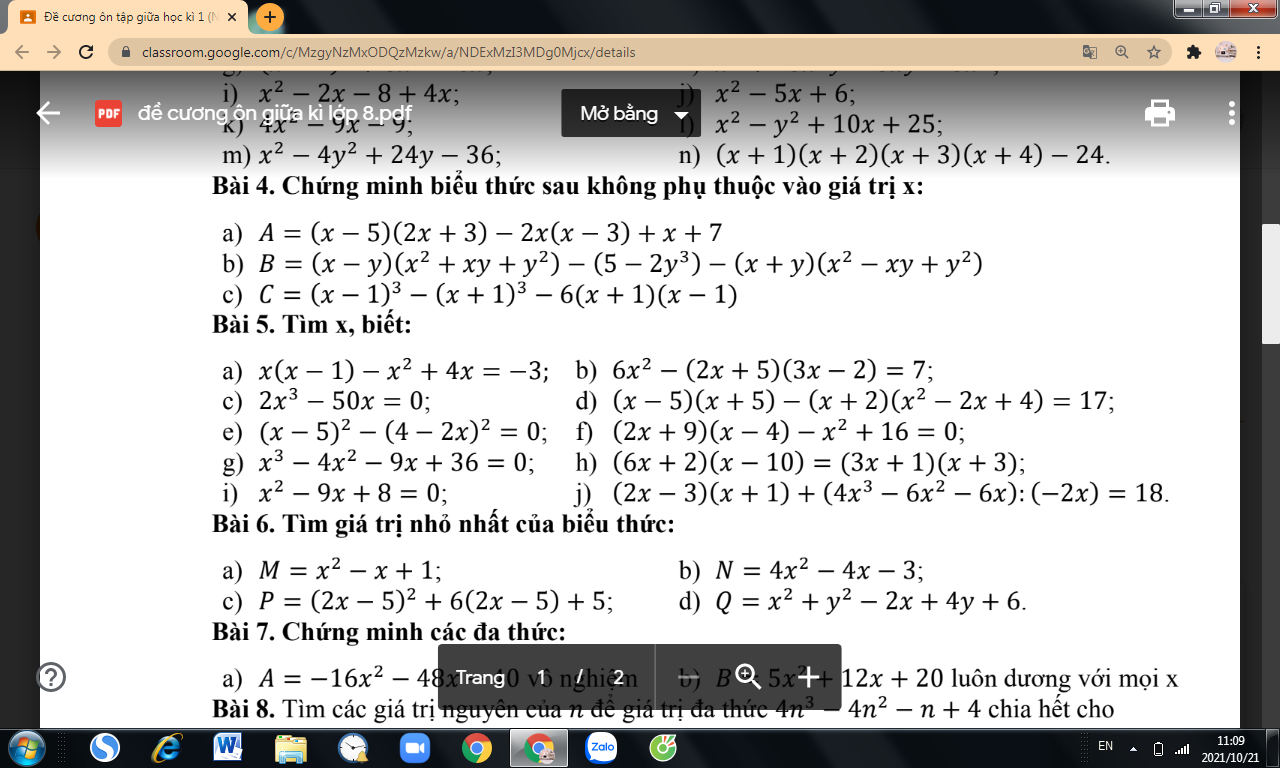
a) \(x\left(x-1\right)-x^2+4x=-3\\ \Rightarrow3x=-3\\ \Rightarrow x=-1\)

b) \(6x^2-\left(2x+5\right)\left(3x-2\right)=7\\ \Rightarrow6x^2-\left(6x^2+15x-4x-10\right)=7\\ \Rightarrow-11x+10=7\\ \Rightarrow x=\dfrac{3}{11}\)

c) \(2x^3-50x=0\\ \Rightarrow2x\left(x^2-50\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x^2-50=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=-5\sqrt{2}\\x=5\sqrt{2}\end{matrix}\right.\)

e) \(\left(x-5\right)^2-\left(4-2x\right)^2=0\\ \Rightarrow\left(x-5\right)^2=\left(4-2x\right)^2\\ \Rightarrow\left[{}\begin{matrix}x-5=4-2x\\x-5=2x-4\end{matrix}\right.\\ \Leftarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)

f) \(\left(2x+9\right)\left(x-4\right)-x^2+16=0\\ \Rightarrow2x^2+9x-8x-36-x^2+16=0\\ \Rightarrow x^2+x-20=0\\ \Rightarrow\left(x-4\right)\left(x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=-5\end{matrix}\right.\) 

mình ko cần câu a,b bn viết lại câu c giúp mình với nó bị mất ở dòng 3,4

Bài 5: 

a: Xét ΔBEC và ΔADC có 

\(\widehat{C}\) chung

\(\widehat{EBC}=\widehat{DAC}\)

Do đó: ΔBEC\(\sim\)ΔADC

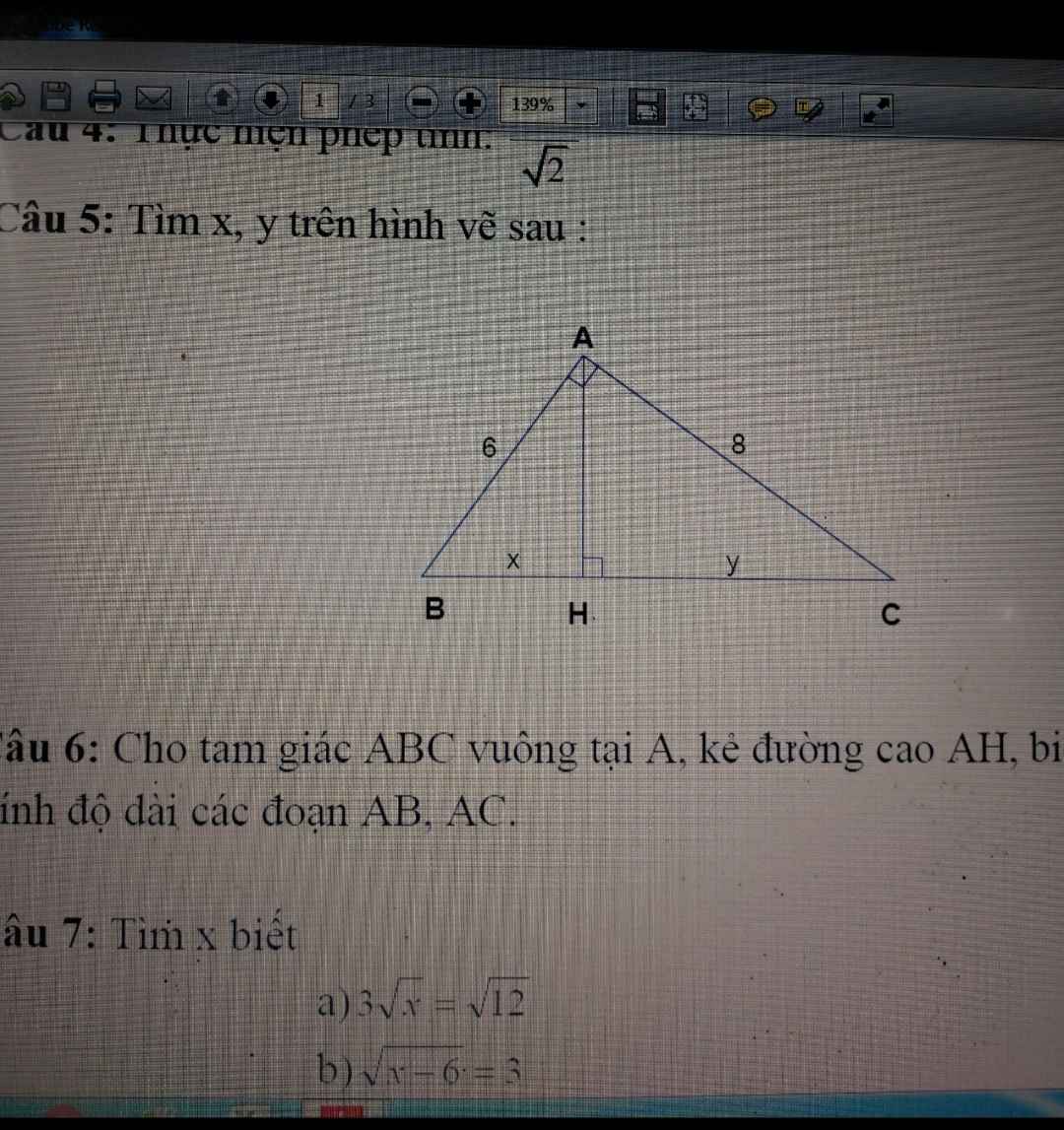
câu 5: 

x=3,6

y=6,4

câu 6: chụp lại đề

câu 7:

a)ĐKXĐ: \(x\ge0\)

\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)

b) ĐKXĐ: \(x\ge6\)

\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)

Câu 5: 

Áp dụng định lý Pi-ta-go ta có:

\(AB^2+AC^2=BC^2\\ \Rightarrow BC=\sqrt{6^2+8^2}\\ \Rightarrow BC=10\)

Áp dụng HTL ta có: \(x.BC=AB^2\Rightarrow x.10=6^2\Rightarrow x=3,6\)

Áp dụng HTL ta có: \(x.BC=AC^2\Rightarrow x.10=8^2\Rightarrow x=6,4\)

Bài 1: hình 2:

áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow20x=144\Rightarrow x=\dfrac{36}{5}\)

\(x+y=BC\Rightarrow\dfrac{36}{5}+y=20\Rightarrow y=\dfrac{64}{5}\)

Bài 2:

hình 4:

BC=BH+HC=1+4=5

áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow1.5=AB^2\Rightarrow x=\sqrt{5}\)

áp dụng HTL ta có: \(HC.BC=AC^2\Rightarrow4.5=AC^2\Rightarrow y=2\sqrt{5}\)

hình 6:

Áp dụng HTL ta có: \(BH.HC=AH^2\Rightarrow4x=25\Rightarrow x=\dfrac{25}{4}\)