Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có: \(\dfrac{-5}{18}+\dfrac{32}{45}-\dfrac{9}{10}\)
\(=\dfrac{-25}{90}+\dfrac{64}{90}-\dfrac{81}{90}\)
\(=\dfrac{-42}{90}=-\dfrac{7}{15}\)
b) Ta có: \(\left(-\dfrac{1}{4}+\dfrac{51}{33}-\dfrac{5}{3}\right)-\left(-\dfrac{15}{12}+\dfrac{6}{11}-\dfrac{42}{29}\right)\)
\(=\dfrac{-1}{4}+\dfrac{17}{11}-\dfrac{5}{3}+\dfrac{5}{4}-\dfrac{6}{11}+\dfrac{42}{29}\)
\(=\dfrac{-5}{3}+\dfrac{42}{29}\)
\(=\dfrac{-145}{87}+\dfrac{126}{87}=\dfrac{-19}{87}\)
c) Ta có: \(1-\dfrac{1}{2}+2-\dfrac{2}{3}+3-\dfrac{3}{4}+4-\dfrac{1}{4}-3-\dfrac{1}{3}-2-\dfrac{1}{2}-1\)
\(=\left(1-1\right)-\left(\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(2-2\right)-\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+\left(3-3\right)-\left(\dfrac{3}{4}+\dfrac{1}{4}\right)+4\)
\(=-1-1-1+4\)
=1
a) Ta có: −518+3245−910−518+3245−910
=−2590+6490−8190=−2590+6490−8190
=−4290=−715=−4290=−715
b) Ta có: (−14+5133−53)−(−1512+611−4229)(−14+5133−53)−(−1512+611−4229)
=−14+1711−53+54−611+4229=−14+1711−53+54−611+4229
=−53+4229=−53+4229
=−14587+12687=−1987=−14587+12687=−1987
c) Ta có: 1−12+2−23+3−34+4−14−3−13−2−12−11−12+2−23+3−34+4−14−3−13−2−12−1
=(1−1)−(12+12)+(2−2)−(23+13)+(3−3)−(34+14)+4=(1−1)−(12+12)+(2−2)−(23+13)+(3−3)−(34+14)+4
=−1−1−1+4=−1−1−1+4
=1
1: \(\dfrac{1}{2}+\dfrac{9}{10}+\dfrac{5}{6}-\dfrac{11}{14}-\dfrac{1}{3}+\dfrac{-4}{35}\)
\(=\left(\dfrac{1}{2}+\dfrac{5}{6}-\dfrac{1}{3}\right)+\dfrac{9}{10}-\left(\dfrac{11}{14}+\dfrac{4}{35}\right)\)
\(=\dfrac{3+5-2}{6}+\dfrac{9}{10}-\dfrac{55+8}{70}\)
\(=1+\dfrac{9}{10}-\dfrac{9}{10}\)
=1
Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.
\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)
b, \(\left(1-\dfrac{1}{100}\right)\left(1-\dfrac{1}{99}\right)...\left(1-\dfrac{1}{2}\right)=\dfrac{99.98...1}{100.99...2}=\dfrac{1}{100}\)
d: \(\left(2^2:\dfrac{4}{3}-\dfrac{1}{2}\right)\cdot\dfrac{6}{5}-17\)
\(=\left(4\cdot\dfrac{3}{4}-\dfrac{1}{2}\right)\cdot\dfrac{6}{5}-17\)
\(=\left(3-\dfrac{1}{2}\right)\cdot\dfrac{6}{5}-17\)
\(=\dfrac{5}{6}\cdot\dfrac{6}{5}-17=1-17=-16\)
h: \(\dfrac{\left(-1\right)^3}{15}+\left(-\dfrac{2}{3}\right)^2:2\dfrac{2}{3}-\left|-\dfrac{5}{6}\right|\)
\(=-\dfrac{1}{15}+\dfrac{-8}{27}:\dfrac{8}{3}-\dfrac{5}{6}\)
\(=-\dfrac{1}{15}-\dfrac{1}{9}-\dfrac{5}{6}\)
\(=\dfrac{-6-10-75}{90}=\dfrac{-91}{90}\)
k: \(\dfrac{2\cdot6^9-2^5\cdot18^4}{2^2\cdot6^8}\)
\(=\dfrac{2^{10}\cdot3^9-2^5\cdot2^4\cdot3^8}{2^2\cdot2^8\cdot3^8}\)
\(=\dfrac{2^{10}\cdot3^9-2^9\cdot3^8}{2^{10}\cdot3^8}=\dfrac{2^9\cdot3^8\left(2\cdot3-1\right)}{2^{10}\cdot3^8}\)
\(=\dfrac{5}{2}\)
n: \(3-\left(-\dfrac{7}{8}\right)^0+\left(\dfrac{1}{2}\right)^3\cdot16\)
\(=3-1+\dfrac{1}{8}\cdot16\)
=2+2
=4
a: \(=\dfrac{28-2-3}{4}:\dfrac{40-2-5}{8}=\dfrac{23}{4}\cdot\dfrac{8}{33}=\dfrac{46}{33}\)
b: =78(0,65+0,35)+2020(2,2-2,2)
=78*1=78
Ta có một số phân tích sau : \(a^4\)\(+\)\(4\)\(=\)\(\left(a^2-2a+2\right)\)\(\left(a^2+2a+2\right)\)
Nhân mỗi biểu thức trong ngoặc ở cả tử thức với \(16\)\(=\)\(2^4\), ta được :
\(A\)\(=\)\(\frac{\left(1+\frac{1}{4}\right)\left(3^4+\frac{1}{4}\right)\left(5^4+\frac{1}{4}\right)...\left(29^4+\frac{1}{4}\right)}{\left(2^4+\frac{1}{4}\right)\left(4^4+\frac{1}{4}\right)\left(6^4+\frac{1}{4}\right)...\left(30^4+\frac{1}{4}\right)}\)
\(A\)\(=\)\(\frac{\left(2^4+4\right)\left(6^4+4\right)\left(10^4+4\right)...\left(58^4+4\right)}{\left(4^4+4\right)\left(8^4+4\right)\left(12^4+4\right)...\left(60^4+4\right)}\)
Kết hợp với phân tích nêu trên, khi đó :
\(A\)\(=\)\(\frac{\left(2^2-2.2+2\right)\left(2^2+2.2+2\right)\left(6^2-2.6+2\right)\left(6^2+2.6+2\right)....\left(58^2-2.58+2\right)\left(58^2+2.58+2\right)}{\left(4^2-2.4+2\right)\left(4^2+2.4+2\right)\left(8^2-2.8+2\right)\left(8^2+2.8+2\right)....\left(60^2-2.60+2\right)\left(60^2+2.60+2\right)}\)
\(\Rightarrow\)\(A\)\(=\)\(\frac{2.10.26.50.82.122....3250.3482}{10.26.50.82.122....3482.3722}\)\(=\)\(\frac{2}{3722}\)\(=\)\(\frac{1}{1861}\)
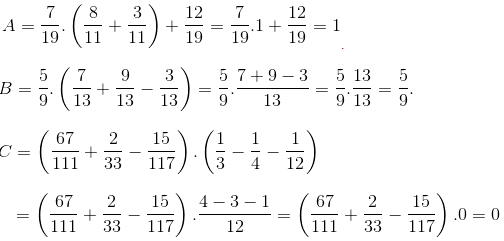
a) Ta có: \(\left(\dfrac{617}{191}+\dfrac{29}{33}-\dfrac{115}{17}\right)\cdot\left(\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{20}\right)\)
\(=\left(\dfrac{617}{191}+\dfrac{29}{33}-\dfrac{115}{17}\right)\cdot\left(\dfrac{5}{20}-\dfrac{4}{20}-\dfrac{1}{20}\right)\)
\(=0\cdot\left(\dfrac{617}{191}+\dfrac{29}{33}-\dfrac{115}{17}\right)=0\)
b) Ta có: \(\dfrac{12}{5}\cdot\left(\dfrac{10}{3}-\dfrac{5}{12}\right)\)
\(=\dfrac{12}{5}\cdot\left(\dfrac{40}{12}-\dfrac{5}{12}\right)\)
\(=\dfrac{12}{5}\cdot\dfrac{35}{12}\)
=7