Ba địa điểm $ {A}, {B}, {C}$ là 3 đỉnh của tam giác $ {ABC}$ với $\widehat{A}=90^{\circ}$ và khoảng cách giữa 2 địa điểm $ {A}$ và $ {C}$ là $550$ m. Người ta đặt một loa truyền thanh tại một địa điểm nằm giữa $ {A}$ và $ {B}$ thì tại $ {C}$ có thể nghe tiếng loa không nếu bán kính để nghe rõ tiếng của loa là $550$ m?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi điểm được đặt là M
=>ΔAMC vuông tại A
=>AC<AM
=>Ko nghe rõ được bởi AM>550m
Gọi D là địa điểm đặt loa truyền thanh
Ta có: góc A=90°
=> AC là đường vuông góc
=> CD là đường xiên
Dó đó: AC<CD
Hay CD>550m( vì AC=550m )
Vậy tại C ko thể nghe rõ tiếng loa

góc B>90 độ
=>góc BMA<90 độ
=>góc CMA>90 độ
=>CA>AM
=>AM<600
=>Ko thể nghe thấy đc

Vì \(\widehat{A} \) là góc tù `=>` Cạnh `BC` là cạnh lớn nhất
`=> BC > AC`
Mà bán kính nghe rõ của loa là `500m`
`=>` Từ khoảng cách đó không thể nghe thấy được.

Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
Vậy khoảng cách AB là 1433,2 m.

Chọn B.
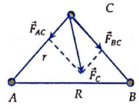
Vì tam giác ABC cân tại C nên ta có AC=BC= R 2
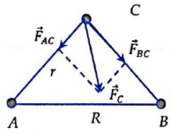
Lực hấp dẫn tác dụng lên chất điểm tại
![]()
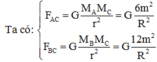
![]()
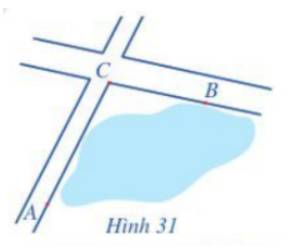


Gọi D là điểm người ta đặt loa phát thanh
Trong `ΔACD` vuông tại A có CD là cạnh huyền `⇒ CD` là cạnh lớn nhất
`⇒ CD > AC`
Mà: `AC = 550(m) `
`⇒CD > 550`
Vậy ở vị trí C không thể nghe rõ được tiếng của loa phát thanh
Gọi D là điểm người ta đặt loa phát thanh
Trong Δ���ΔACD vuông tại A có CD là cạnh huyền ⇒��⇒CD là cạnh lớn nhất
⇒��>��⇒CD>AC
Mà: ��=550(�)AC=550(m)
⇒��>550⇒CD>550
Vậy ở vị trí C không thể nghe rõ được tiếng của loa phát thanh