Cho ${x}, {y}, {z} \neq 0$ và ${x}-{y}-{z}=0$. Tính giá trị của biểu thức ${B}=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ \(x\left(\dfrac{1}{y}+\dfrac{1}{z}\right)+y\left(\dfrac{1}{z}+\dfrac{1}{x}\right)+z\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=-2\) ta có:
\(x^2y+y^2z+z^2x+xy^2+yz^2+zx^2+2xyz=0\)
\(\Leftrightarrow\left(x+y\right)\left(y+z\right)\left(z+x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\z+x=0\end{matrix}\right.\).
Không mất tính tổng quát, giả sử x + y = 0
\(\Leftrightarrow x=-y\)
\(\Leftrightarrow x^3=-y^3\).
Kết hợp với \(x^3+y^3+z^3=1\) ta có \(z^3=1\Leftrightarrow z=1\).
Vậy \(P=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{-y}+\dfrac{1}{y}+\dfrac{1}{1}=1\).

x+y+z=0
nên x+y=-z; y+z=-x; x+z=-y
\(\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)\)
\(=\dfrac{x+y}{y}\cdot\dfrac{y+z}{z}\cdot\dfrac{x+z}{x}=-1\)

Lời giải:
\(A=\left(\frac{x}{y-z}+\frac{y}{z-x}+\frac{z}{x-y}\right)\left(\frac{1}{y-z}+\frac{1}{z-x}+\frac{1}{x-y}\right)-\frac{x}{(y-z)(z-x)}-\frac{x}{(y-z)(x-y)}-\frac{y}{(z-x)(x-y)}-\frac{y}{(z-x)(y-z)}-\frac{z}{(x-y)(y-z)}-\frac{z}{(x-y)(z-x)}\)
\(=0-\frac{x(x-y)+x(z-x)+y(y-z)+y(x-y)+z(z-x)+z(y-z)}{(x-y)(y-z)(z-x)}\)
\(=0-\frac{x^2+xz+y^2+xy+z^2+zy-(xy+x^2+yz+y^2+zx+z^2)}{(x-y)(y-z)(z-x)}=0-\frac{0}{(x-y)(y-z)(z-x)}=0\)
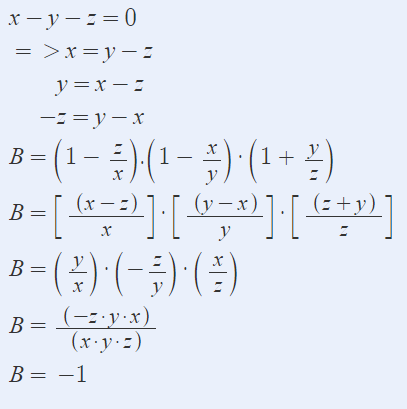
Với \(x,y,z\ne0\), ta có: \(x-y-z=0\Leftrightarrow\left\{{}\begin{matrix}x-z=y\\y-x=-z\\z+y=x\end{matrix}\right.\)\((*)\)
Mặt khác: \(B=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}\)
Thay \((*)\) vào \(B\), ta được:
\(B=\dfrac{y}{x}\cdot\dfrac{-z}{y}\cdot\dfrac{x}{z}=-1\)
Vậy \(B=-1\) thoả mãn đề bài.
+ \(x-y-z=0\)
\(\Rightarrow\dfrac{x}{x}-\dfrac{\left(y+z\right)}{x}=0\) (Do \(x\ne0\))
\(\Leftrightarrow1-\dfrac{y+z}{x}=0\)
+ \(x-y-z=0\)
\(\Rightarrow\dfrac{\left(x-z\right)}{y}-\dfrac{y}{y}=0\) (Do \(y\ne0\))
\(\Leftrightarrow1-\dfrac{x-z}{y}=0\)
+ \(x-y-z=0\)
\(\Rightarrow\dfrac{\left(x-y\right)}{z}-\dfrac{z}{z}=0\) (Do \(z\ne0\))
\(\Leftrightarrow1-\dfrac{x-y}{z}=0\)
Ta có: \(B=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\left(1-\dfrac{x}{y}-\dfrac{z}{x}+\dfrac{zx}{xy}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\left(1-\dfrac{x}{y}-\dfrac{z}{x}+\dfrac{z}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=1+\dfrac{y}{z}-\dfrac{x}{y}-\dfrac{xy}{yz}-\dfrac{z}{x}-\dfrac{zy}{xz}+\dfrac{z}{y}+\dfrac{zy}{yz}\)
\(=1-\dfrac{y+z}{x}+1-\dfrac{x-z}{y}+1-\dfrac{x-y}{z}-1\)
\(=-1\)
Vậy \(B=-1\)