Câu 2: Chọn kết luận đúng:
A.
B.
C.
D.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Vì \(y=\sqrt{2}\) là hàm hằng nên với mọi giá trị của \(x\) thì đều nhận \(\sqrt{2}\) là giá rị của \(y\)
\(\Rightarrow B\)
2. \(D\)
3.
Giải hệ \(\left\{{}\begin{matrix}\dfrac{1}{2}\left(x+2\right)\left(y+3\right)=\dfrac{1}{2}xy+50\\\dfrac{1}{2}\left(x-2\right)\left(y-2\right)=\dfrac{1}{2}xy-32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=26\\y=8\end{matrix}\right.\)
\(\Rightarrow xy=208\Rightarrow A\)
4.
\(\overrightarrow{AM}.\overrightarrow{AN}=-a^2\)
5.
\(\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)
6. \(C\)
Câu 4: Đáp án
A. \(2a^2\) B.\(a^2\) C.\(\frac{1}{2}a^2\) D.\(\frac{-1}{2}a^2\)
Không có đáp án \(-a^2 \)

Chọn đáp án C và D. Thỏa mãn 2 điều kiện chứng minh một tia là tia phân giác là : Tia nằm giữa và tạo với hai cạnh hai góc bằng nhau.

Khi nhân cả hai vế của bất đẳng thức với cùng một số dương, ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Từ đó với a > b và c > 0 thì ac > bc nên A đúng.
Đáp án cần chọn là: A

Ta có:
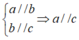
(hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau)
Chọn đáp án A.

c35:
a,tứ giác AMDN là hình chữ nhật vì
góc DMA=MAN=DNA=90\(^o\)
b,
áp dụng đl pytago vào tam giác vuông DMA có:
\(MD^2=DA^2-AM^2\\ MD=\sqrt{5^2-3^2}=4cm\)
\(S_{DMA}=\dfrac{MD.AM}{2}=\dfrac{4.3}{2}=6cm^2\)
vì AMDN là hình chữ nhật nên:
AM=DN=3cm
\(S_{AND}=\dfrac{DN.AN}{2}=6cm^2\)
\(S_{AMDN}=S_{AMD}+S_{AND}=6+6=12cm^2\)
C36:
a, xét tứ giác ADME có:
góc MDA=DAE=MEA=90\(^o\)
nên ADME là hình chữ nhật
b, xét tam giác ABC có:
\(ME\perp AC\\ AB\perp AC\\ \Rightarrow ME//AB\)
mà M là trung điểm BC nên :
E là trung điểm AC
\(MD\perp AB\\ AC\perp AB\\ \Rightarrow MD//AC\)
mà M là trung điểm BC nên:
D là trung điểm AB
xét tam giác ABC có đường t/b DE nên:
DH//EC và DH=EC
=>CMDE là hình bình hành
c,ta có:
DE là đường t/b của ABC nên:
DE//HM
=>MHDE là hình thang(1)
ta có:
góc BDH+HDE+EDA=180\(^o\)
góc DEA+MED+MEC=180\(^o\)
(BDH+HDE+EDA=DEA+MED+MEC=180\(^o\))
mà BDH+EDA=MEC+DEA(gt)
=>HDE=MED(2)
từ (1)và (2) suy ra:
tứ giác MHDE là hình thang cân

ΔABC và ΔDEF có góc B = D; B A B C = D E D F thì ΔABC đồng dạng với ΔEDF
Đáp án: B
A. \(\dfrac{-7}{12}=\dfrac{-2}{15}\) (sai)
B. \(\dfrac{7}{15}>\dfrac{-2}{15}\) (đúng)
C. \(\dfrac{-7}{15}< \dfrac{-2}{15}\) (đúng)
D. \(\dfrac{-7}{15}>\dfrac{-2}{15}\) (sai)
⇒ Chọn B và C