Tìm số tự nhiên nhỏ nhất sao cho khi chia cho và chia cho ta đều được kết quả là số tự nhiên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Vì khi chia n cho \(\dfrac{6}{7}\) và chia n cho \(\dfrac{3}{4}\) ta đều đc kết quả là số tự nhiên nên ta có:
n ⋮ \(\dfrac{6}{7}\)
n ⋮ \(\dfrac{3}{4}\) ⇒n ∈ BCNN(6;3)
n nhỏ nhất
6=2.3
3=3
⇒BCNN(6;3)=2.3=6
Vậy số tự nhiên n khác 0 nhỏ nhất là 6.
Chúc bạn học tốt!
theo bài ra , ta có :
- a : \(\dfrac{6}{7}\) = \(\dfrac{7n}{6}\) \(\in\) N \(\Rightarrow\) 7n chia hết cho 6 .
Mà ƯCLN ( 7 ; 6 ) = 1 \(\Rightarrow\) n chia hết cho 6 . ( 1 )
- n : \(\dfrac{3}{4}\) = \(\dfrac{4n}{3}\) \(\in\) N \(\Rightarrow\) 4n chia hết cho 3 . ( 2 )
Mà ƯCLN ( 4 ; 3 ) = 1 \(\Rightarrow\) n chia hết cho 3 . ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\) n \(\in\) BC ( 6 ; 3 ) .
Mà n nhỏ nhất \(\Rightarrow\) n = BCNN ( 6 ; 3 ) = 6 .
Vậy số cần tìm là 6 .

Theo bài ra, ta có:
+a : \(\frac{6}{7}\) =\(\frac{7a}{6}\) thuộc N => 7a chia hết cho 6
Mà UCLN(7,6)=1 => a chia hết cho 6 (1)
+a : \(\frac{10}{11}\) = \(\frac{11a}{10}\) thuộc N => 11a chia hết cho 10
Mà UCLN(11, 10) =1 => a chia hết cho 10 (2)
Từ (1) và (2) => a thuộc BC(10,6)
Mà a nhỏ nhất => a =BCNN(10,6) => a =30
Vậy số cần tìm là 30
k cho mình nha

a/(6/7) = 7a/6;
a/(10/11) = 11a/10;
vì 7 không chia hết cho 6 nên a phải chia hết cho 6
vì 11 không chia hết cho 10 nên a phải chia hết cho 10
mà a nhỏ nhất
=> a là bcnn(6,10) => a=60
Theo đề bài a :6/7 = a . 7/6 thuộc N nên 7a chia hết cho 6 nên suy ra a chia hết cho 6 (vì 7 và 6 nguyên tố cùng nhau): a : 10/11 = a. 11/10 thuộc N nên 11a chia hết cho 10 suy ra a chia hết cho 10 ( vì 11 và 10 nguyên tố cùng nhau). Như vậy a là bội chung của 6 và 10.
Để a nhỏ nhất thì a = BCNN (6 ;10) = 30
Vậy số phải tìm là 30
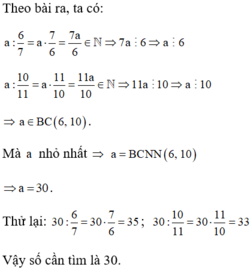
n=0 rồi thì cần gì tìm nữa hả bạn?