F(x)=x*3+x*2+(2a+3)x-3a chia x-2 dư 14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi thương trong phép chia
+) f(x) cho (x-1) là g(x)
+) f(x) cho (x-2) là h(x)
Theo đề bài ta có : \(\hept{\begin{cases}f\left(x\right)=\left(x-1\right)\cdot g\left(x\right)+4\left(I\right)\\f\left(x\right)=\left(x-2\right)\cdot h\left(x\right)+13\left(II\right)\end{cases}}\)
Thay x = 1 vào (I) ta được 1 + a + b = 4 => a + b = 3 (1)
Thay x = 2 vào (II) ta được 8 + 2a + b = 13 => 2a + b = 5 (2)
Từ (1) và (2) ta có hệ \(\hept{\begin{cases}a+b=3\\2a+b=5\end{cases}}\Rightarrow\hept{\begin{cases}a=2\\b=1\end{cases}}\)
=> 3a + 2b = 3.2 + 2.1 = 6 + 2 = 8

Áp dụng định lý Bezout ta có:
f(x) chia hết cho x-3 \(\Rightarrow f\left(3\right)=0\)
\(\Leftrightarrow2a+3b=-87\left(1\right)\)
g(x) chia hết cho x-3 \(\Rightarrow g\left(3\right)=0\)
\(\Leftrightarrow-3a+2b=-318\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\hept{\begin{cases}2a+3b=-87\\-3a+2b=-318\end{cases}\Leftrightarrow}\hept{\begin{cases}a=60\\b=-69\end{cases}}\)
Vậy ...

Lời giải:
Theo định lý Bê-du về phép chia đa thức thì số dư của $f(x)$ chia cho $x-a$ có số dư là $f(a)$.
Áp dụng vào bài:
$f(2)=8a+4b+10=14\Leftrightarrow 2a+b=1(1)$
$f(-1)=-a+b-14=-16\Leftrightarrow -a+b=-2(2)$
Từ $(1); (2)\Rightarrow a=1; b=-1$

f(x)= (x-3). Q(x)+2 moi X
f(x)=(x+4).H(x)+9 moi X
=>f(3)= 2
f( -4)= 9
f(x)= (x^2+x-12).(x^2+3)+ ax +b
=(x-3)(x+4). (x^2+3) +ax+b
=>f(3)= 3a+b=2
f(-4)=b -4a=9
=>a= -1; b=5
=> f(x)=(x^2+x-12)(x^2+3)-x+5
= x^4+x^3-9x^2+2x-31
Ta thấy :
x2 +x -12 = x2 +4x - 3x-12
= x(x+4) - 3(x+4)
= (x-3)(x+4)
Vì :
f(x) chia (x-1)(x+4) được x2 + 3 và còn dư
Mà số dư có bậc không vượt quá 1
=> f(x) = (x-3)(x+4)(x2 + 3) +ax +b
Ta có :
f(x) chia (x-3) dư 2
=> f(3)=2
=> 3a+b=2
f(x) chia (x+4) dư 9
=> f(-4)=9
=> b-4a=9
=> 3a+b-b+4a = 2-9
7a = -7
=> a= -1
=> -3 + b =2
b=5
Vậy đa thức f(x) = (x-3)(x+4)(x2 + 3) - x + 5
Đa thức f(x) chia cho (x-2) dư 6, chia cho (x²+3)dư 3x+2
Tìm đa thức dư f(x) chia cho (x-2) . (x²+3)

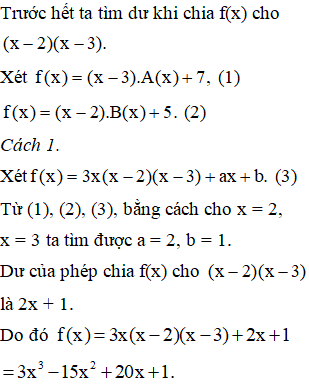
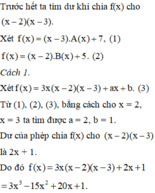
Lời giải:
$F(x)=x^3+x^2+(2a+3)x-3a=x^2(x-2)+3x(x-2)+(2a+9)x-3a$
$=x^2(x-2)+3x(x-2)+(2a+9)(x-2)+2(2a+9)-3a$
$=(x-2)(x^2+3x+2a+9)+(a+18)$
$\Rightarrow F(x)$ chia $x-2$ dư $a+18$
Để số dư là $14$
$\Rightarrow a+18=14$
$\Rightarrow a=-4$