Cho AOB = 50 độ , có tia phân giác OC.Gọi OD là tia đối của tia OC . Trên nửa mặt phẳng bờ CD chứa OA, vẽ tia DE sao cho góc DOE = 25 độ .Tìm góc đối đỉnh với DOE(có giải thích)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đề bài yêu cầu "tìm" nên mình chỉ cần chỉ ra thôi phải không bạn?
Vì vậy góc đối đỉnh với góc DOE là góc COB(theo hình vẽ)
nếu đúng thì tick đúng cho mình nhé

Góc đối đỉnh với \(\widehat{DOE}\)là \(\widehat{BOC}\)
P/s : ko chắc
+ Vì \(\widehat{COB}\)và \(\widehat{BOD}\)kề bù nên \(\widehat{COB}+\widehat{BOD}=180^o\)(1)
+ Vì \(\widehat{COE}\)và \(\widehat{DOE}\)kề bù nên \(\widehat{COE}+\widehat{DOE}=180^o\)(2)
Từ (1) và (2) suy ra: \(\widehat{COB}\)đối đỉnh \(\widehat{DOE}\)và \(\widehat{COB}=25^o\)

Hình vẽ:
Giải:
Vì OD là tia đối của tia OC
Nên \(\widehat{COD}=180^0\)
Lại có OC là tia phân giác của \(\widehat{AOB}\)
Nên \(\widehat{AOC}=\widehat{COB}=\dfrac{1}{2}\widehat{AOB}=\dfrac{1}{2}.50^0=25^0\)
Vì \(\widehat{COD}>\widehat{COB}\left(180^0>25^0\right)\)
Nên OB là tia nằm giữa hai tia OC và OD
\(\Leftrightarrow\widehat{COB}+\widehat{BOD}=\widehat{COD}\)
Hay \(25^0+\widehat{BOD}=180^0\)
\(\Rightarrow\widehat{BOD}=180^0-25^0=155^0\)
Vì hai tia OE và OB nằm trên hai nửa mặt phẳng khác nhau có bờ là CD
Nên hai góc \(\widehat{DOE}\) và \(\widehat{BOD}\) là hai góc kề nhau
Mà \(\widehat{DOE}=25^0\); \(\widehat{BOD}=155^0\)
\(\Leftrightarrow\widehat{DOE}+\widehat{DOB}=25^0+155^0=180^0\)
Hay \(\widehat{BOE}\) là góc bẹt
\(\Rightarrow\) Tia OB là tia đối của tia OE
Mặt khác: Tia OD là tia đối của tia OC
\(\Leftrightarrow\widehat{DOE}=\widehat{COB}=25^0\) (Hai góc đối đỉnh)
Vậy góc đối đỉnh với \(\widehat{DOE}\) là \(\widehat{COB}\).
Chúc bạn học tốt!!!
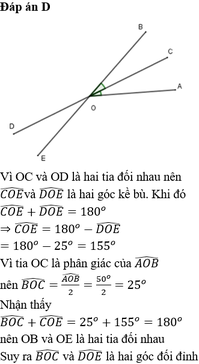
Vì OC là tia phân giác của \(\widehat{AOB}\) nên \(\widehat{AOC}=\widehat{COB}=\frac{\widehat{AOB}}{2}=\frac{50^o}{2}\) = 25o
Ta thấy \(\widehat{COB}=\widehat{EOD}\) và OC là tia đối của OD nên => \(\widehat{COB}\) đối đỉnh với \(\widehat{DOE}\)