chứng minh rằng aaaa:aa bằng 101
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong các số nguyên đã cho có ít nhất một số nguyên âm .
Thật vậy , nếu các số đã cho đều là các số nguyên không âm thì tổng của 25 số bất kì là số nguyên không âm .Điều này mâu thuẫn với đề bài toán.
Tách riêng số nguyên âm này ra , còn lại 100 số , chia 100 số này thành 4 nhóm , mỗi nhóm 25 số. Theo đầu bài , ta có tổng của các số của mỗi nhóm là số nguyên âm nên tổng của các số của nhóm và số nguyên âm tách ra là số nguyên âm.
Do vậy tổng của 101 số nguyên đã cho là số nguyên âm

Trong các số nguyên đã cho có ít nhất một số nguyên âm .
Thật vậy , nếu các số đã cho đều là các số nguyên không âm thì tổng của 25 số bất kì là số nguyên không âm .Điều này mâu thuẫn với đề bài toán.
Tách riêng số nguyên âm này ra , còn lại 100 số , chia 100 số này thành 4 nhóm , mỗi nhóm 25 số. Theo đầu bài , ta có tổng của các số của mỗi nhóm là số nguyên âm nên tổng của các số của nhóm và số nguyên âm tách ra là số nguyên âm.
Do vậy tổng của 101 số nguyên đã cho là số nguyên âm


Gọi 51 số đó là a1;a2;a3;...;a50;a51
Không làm mất tính tổng quát, ta giả sử \(a_1< a_2< a_3< ...< a_{51}\)(nhóm số 1 có 51 số)
Xét nhóm số thứ 2 có 51 hiệu: \(100-a_1>100-a_2>100-a_3>...>100-a_{51}\)
Tổng cộng 2 nhóm có 102 số mà 102 số này không quá 100 và khác 0 nên chúng nhận các giá trị 1;2;3;...;100 có 100 giá trị. Vậy theo nguyên lí Đi-rích-lê thì có [102/100]+1=2 số nhận cùng 1 giá trị. Mà hai số này hiển nhiên không thuộc cùng 1 nhóm nên nó sẽ thuộc hai nhóm khác nhau. Gọi chúng là 101-\(a_m\)=\(a_n\) suy ra 100=\(a_m+a_n\)hay ta có đpcm
Sửa khúc cuối nhé!: Gọi hai số đó là \(a_n;101-a_m\left(1\le m;n\le51\right)\Rightarrow a_n=101-a_m\)hay \(a_m+a_n=101\)vậy ta có đpcm


Bài 1: \(\overline{abcd}\) ⋮ 101
⇒ \(\overline{ab}\) \(\times\) 100 + \(\overline{cd}\) ⋮ 101
\(\overline{ab}\) \(\times\) 101 - \(\overline{ab}\) + \(\overline{cd}\) ⋮ 101
\(\overline{ab}\) \(\times\) 101 - (\(\overline{ab}\) - \(\overline{cd}\)) ⋮ 101
\(\overline{ab}\) - \(\overline{cd}\) ⋮ 101 (đpcm)

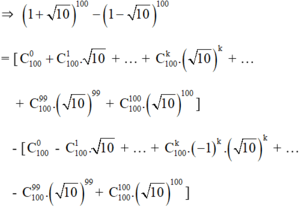
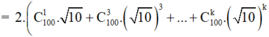
Ta có :
\(\overline{aaaa}:\overline{aa}=1111.a:\left(11.a\right)\)
\(\Rightarrow\overline{aaaa}:\overline{aa}=\frac{1111.a}{11.a}\)
\(\Rightarrow\overline{aaaa}:\overline{aa}=\frac{1111}{11}=101\)\(\left(đpcm\right)\)