Cho hình vuông ABCD nội tiếp đường tròn (O; R), cho hình vuông ABCD quay xung quanh đường trung trực của 2 cạnh đối, thì phần thể tích của khối cầu nằm ngoài khối trụ là:
A. \(\frac{\pi R^3}{4}\left(8-3\sqrt{2}\right)\) B. \(\frac{\pi R^3}{6}\left(8-3\sqrt{3}\right)\) C. \(\frac{\pi R^3}{3}\left(8-3\sqrt{2}\right)\) D.\(\frac{\pi R^3}{12}\left(8-3\sqrt{2}\right)\)
( Có lời giải )


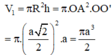
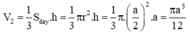
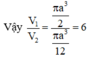


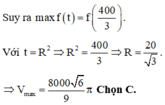

Thể tích khối cầu là: \(\frac{4}{3}\pi R^3\)
Độ dài cạnh hình vuông là: \(R\sqrt{2}\).
Thể tích của khối trụ là: \(\left(\frac{R\sqrt{2}}{2}\right)^2\pi\left(R\sqrt{2}\right)=\frac{\pi R^3\sqrt{2}}{2}\)
Phần thể tích khối cầu nằm ngoài khối trụ là: \(\frac{\pi R^3}{6}\left(8-3\sqrt{2}\right)\).