BN CÓ THỂ GIẢI THEO 1 TRONG 3 CÁCH SAU

• CÁCH 1:
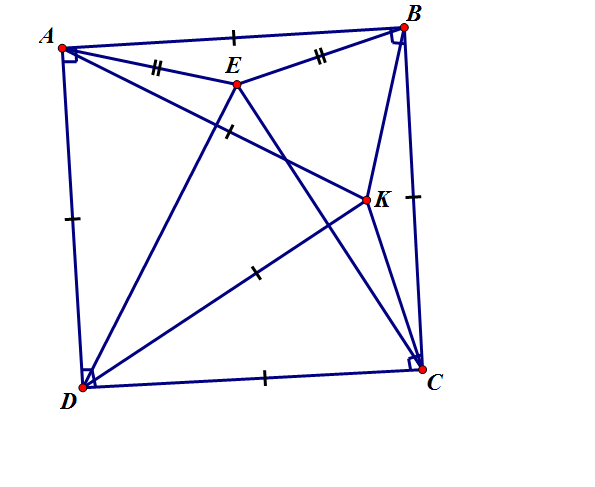
• vẽ tam giác đều ADK(K và B cùng phía với AD)
• =>ˆDAKDAK^=60∘60∘=>ˆKABKAB^=90∘90∘-60∘=30∘60∘=30∘.

• ΔABKΔABK cân tại A=>ˆABK=75∘ABK^=75∘=>KBC=90∘−75∘=15∘90∘−75∘=15∘
• tương tự 
• ΔDKCΔDKCcân tại D=>ˆDKC=180∘−30∘2=75∘DKC^=180∘−30∘2=75∘=>ˆKCB=15∘KCB^=15∘

• có ΔAEB=ΔBKCΔAEB=ΔBKC(g.c.g)=>AE=BK=KCΔADE=ΔKDCΔADE=ΔKDC(c.g.c)
• =>DE=DC(1), ˆADE=ˆKDC=30∘ADE^=KDC^=30∘=>ˆEDC=60∘EDC^=60∘ (2)

 (1),(2)→ΔEDC đều

• ​
• CÁCH 2
•  Dựng tam giác đều DME (M trong tam giác ADE)
•  MDA=15∘⇒ΔADM=ΔCDE(c.g.c)⇒AM=CE=DE=DM⇒ˆMAD=15∘⇒ˆAMD=150∘⇒ˆAME=150∘⇒ΔAMD=ΔAME(c.g.c)⇒AE=AD=AB⇒MDA^=15∘⇒ΔADM=ΔCDE(c.g.c)⇒AM=CE=DE=DM⇒MAD^=15∘⇒AMD^=150∘⇒AME^=150∘⇒ΔAMD=ΔAME(c.g.c)⇒AE=AD=AB
• Tính được ˆBAE=60∘→BAE^=60∘→ tam giác ABE là tam giác đều
• ​CÁCH 3 

• :-Lấy E' trong hình vuông ABCD sao cho tam giác DCE' đều.

  -Ta có: DE'=DA và góc ADE'= 30 độ.

  => góc DAE'= 75 độ. Và có góc DAB=90 độ.

  => góc BAE'= 15 độ.

  -Chứng minh tương tự, ta có góc ABE'=15 độ.

  Suy ra điểm E trùng với E'.

   Vậy tam giác DEC đều.

• NHỚ TK MK NHA,

Dài thế! nhưng thôi cho bạn 1 k

vì tam giác ABE đều nên góc ABE = AEB = 60⁰

suy ra goc EBC = 90 - 30 = 60⁰

vì tam giác BFC đều nên goc FBC = FCB = 60^o

Ta có tam giác EBF cân tại B (vì BE =BF ) và goc EBF = EBC + CBF = 60+30 = 90^o

suy ra goc BEF = \(\frac{180-90}{2}\)=45^o

ta có goc AEF = AEB + BEF = 60 + 45 = 105^o

ta có tam giac AED cân tại A(vì AD = AE) và goc EAD = 30^o nên goc AED = \(\frac{180-30}{2}\)= 75^o

Ta có goc AED + goc AEF = 75 + 105 = 180^o

suy ra D, E, F thẳng hàng

Giả sử tứ giác ABCD định hướng âm. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{3}\) ta có

\(\overrightarrow{EG}=\overrightarrow{AG}-\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BG}-\overrightarrow{AE}\)

suy ra \(f\left(\overrightarrow{EG}\right)=f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{BG}\right)-f\left(\overrightarrow{AE}\right)\)

                        \(=\overrightarrow{AE}+\overrightarrow{BC}-\overrightarrow{BE}\)

                        \(=\overrightarrow{AC}\)

Tương tự ta cũng chứng minh được \(f\left(\overrightarrow{HF}\right)=\overrightarrow{AC}\)

Từ đó suy ra \(\overrightarrow{EG}=\overrightarrow{HF}\)

Do đó tứ giác EGFH là hình bình hành

Bài làm

Vì tam giác NAB và tam giác đều

=> NA = NB = BA

=> Góc N = góc NBA = góc NAB = 60^o 

Ta có: Góc ABM = NAB + N ( tính chất goác ngoài tam giác )

   hay  Góc ABM = 60^o + 60^o 

   =>    Góc ABM = 120^o 

Lại có: Góc ABC + CBM = ABM 

      hay góc ABC + 15^o = 120^o 

       => Góc ABC = 120^o - 15^o 

       => Góc ABC = 105^o 

Ta có: Góc NBM = ABN + ABC + CBM 

     hay góc NBM = 60^o + 105^o + 15^o 

      =>  góc NBM = 180^o 

Do đó góc NBM là góc bẹt

=> 3 điểm B, M, N thẳng hàng ( đpcm )

# Chúc bạn học tốt #

hình như bạn vẽ sai hình thì phải.