 các bạn giúp mik 1 câu cux đc ạ
các bạn giúp mik 1 câu cux đc ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xet ΔABC có AD/AB=AE/AC
nên DE//CB
b: DE//BC
AH vuông góc BC
=>AH vuông góc DE
ΔADE cân tại A
mà AH là đường cao
nên AH là trung trực của DE
c: ΔCBA đều
mà BF là trung tuyến
nên BF vuông góc AC

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40


Xét tam giác ABC có: góc A+góc B+góc C=180o
=>Góc B+góc C=180o-góc A=180o-60o=120o
Tổng tia phân giác của góc B và góc C là (góc B)/2+(góc C)/2
=(góc B+góc C)/2=120o/2=60o=>góc IBC+góc ICB=60o
Xét tam giác BIC có: góc IBC+góc ICB+góc BIC=180o
=>Góc BIC=180o-(góc IBC+góc ICB)=180o-60o=120o
Vậy góc BIC=60o


9.
a, \(x^4-x^3-14x^2+x+1=0\)
\(< =>x^4+3x^3-x^2-4x^3-12x^2+4x-x^2-3x+1=0\)
\(< =>x^2\left(x^2+3x-1\right)-4x\left(x^2+3x-1\right)-\left(x^2+3x-1\right)=0\)
\(< =>\left(x^2-4x-1\right)\left(x^2+3x-1\right)=0\)
\(=>\left[{}\begin{matrix}x^2-4x-1=0\left(1\right)\\x^2+3x-1=0\left(2\right)\end{matrix}\right.\)
giải pt(1) \(=>x^2-4x+4-5=0< =>\left(x-2\right)^2-\sqrt{5}^2=0\)
\(=>\left(x-2-\sqrt{5}\right)\left(x-2+\sqrt{5}\right)=0\)
\(=>\left[{}\begin{matrix}x=2+\sqrt{5}\\x=2-\sqrt{5}\end{matrix}\right.\)
giải pt(2) \(\)\(=>x^2+3x-1=0< =>x^2+2.\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{13}{4}=0\)
\(< =>\left(x+\dfrac{3}{2}\right)^2-\left(\dfrac{\sqrt{13}}{2}\right)^2=0\)
\(=>\left(x+\dfrac{3}{2}+\dfrac{\sqrt{13}}{2}\right)\left(x+\dfrac{3}{2}-\dfrac{\sqrt{13}}{2}\right)=0\)
tương tự cái pt(1) ra nghiệm rồi kết luận
b, đặt \(\sqrt{x^2+1}=a\left(a\ge1\right)=>x^2+1=a^2\)
\(=>x^4=\left(a^2-1\right)^2\)
\(=>pt\) \(\left(a^2-1\right)^2+a^2.a-1=0\)
\(=>a^4-2a^2+1+a^3-1=0\)
\(< =>a^4-2a^2+a^3=0< =>a^2\left(a+2\right)\left(a-1\right)=0\)
\(->\left[{}\begin{matrix}a=0\left(ktm\right)\\a=-2\left(ktm\right)\\a=1\left(tm\right)\end{matrix}\right.\)rồi thế a vào \(\sqrt{x^2+1}\)
\(=>x=0\)

chủ ngữ they thì bỏ cũng được không bỏ cũng không sao =))

 giúp tớ với mai tớ nộp rồi làm câu b và c cux đc ạ.
giúp tớ với mai tớ nộp rồi làm câu b và c cux đc ạ.
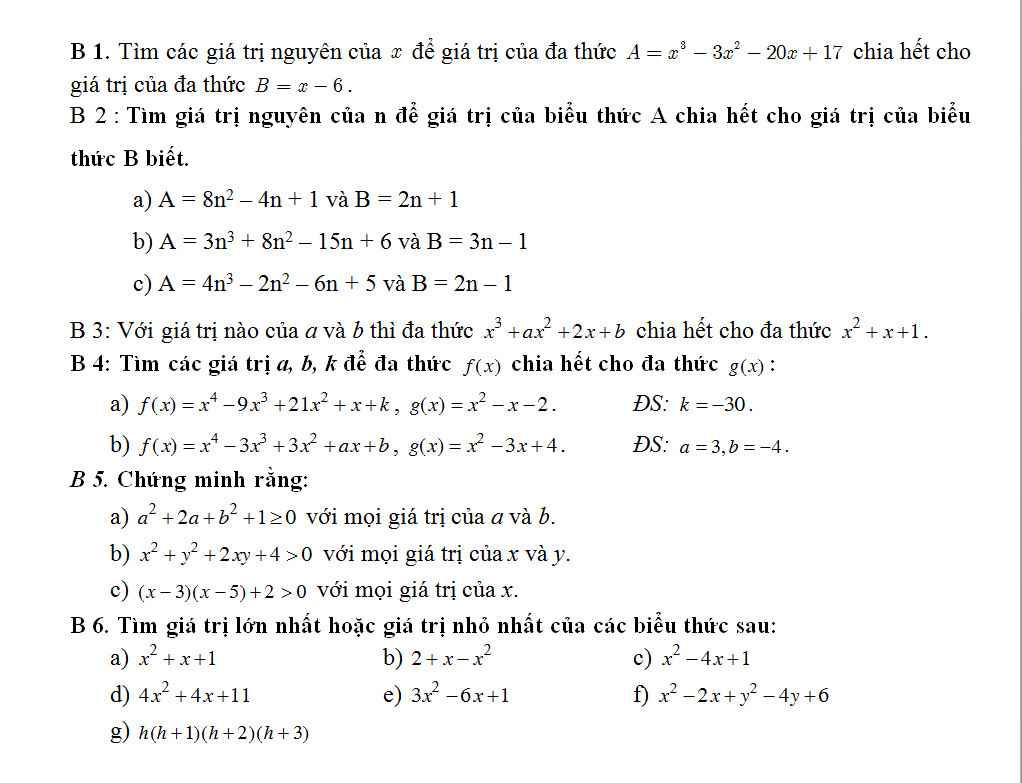

 Giúp em với, chon 1 hay 2 bài cux đc ạ
Giúp em với, chon 1 hay 2 bài cux đc ạ
a: \(A=\dfrac{5}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)+\dfrac{5}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)\)
\(=\dfrac{5}{9}:\dfrac{-3}{22}+\dfrac{5}{9}:\dfrac{1-10}{15}\)
\(=\dfrac{5}{9}\cdot\dfrac{-22}{3}+\dfrac{5}{9}\cdot\dfrac{-5}{3}\)
\(=\dfrac{5}{9}\left(-\dfrac{22}{3}-\dfrac{5}{3}\right)=\dfrac{5}{9}\cdot\left(-9\right)=-5\)
b: \(B=\dfrac{4^5\cdot9^4-2\cdot6^9}{2^{10}\cdot3^8+6^8\cdot20}\)
\(=\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^{10}\cdot3^8\cdot5}\)
\(=\dfrac{2^{10}\cdot3^8\left(1-3\right)}{2^{10}\cdot3^8\left(1+5\right)}=\dfrac{-2}{6}=-\dfrac{1}{3}\)
c: \(C=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}}{\dfrac{2023}{1}+\dfrac{2022}{2}+...+\dfrac{1}{2023}}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}}{\left(1+\dfrac{2022}{2}\right)+\left(1+\dfrac{2021}{3}\right)+...+\left(1+\dfrac{1}{2023}\right)+1}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}}{\dfrac{2024}{2}+\dfrac{2024}{3}+...+\dfrac{2024}{2024}}\)
\(=\dfrac{1}{2024}\)