Cho tam giác ABC nhọn hai đường trung tuyến BM CN cắt nhau tại g a biết BM = 15 cm Tính bgb Trên tia BM lấy điểm E sao cho M là trung điểm B E Chứng minh tam giác ABM bằng tam giác cme Từ đó suy ra AB song song CE C Chứng minh ai song song bc d qua B kẻ đường thẳng song song AC cắt CN tại f Chứng minh aef thẳng hàng và a là trung điểm Fe
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
Xét ΔBAC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>BG=2/3BM và CG=2/3CN
BG+CG>BC
=>2/3BM+2/3CN>BC
=>2/3(BM+CN)>BC
=>BM+CN>3/2BC
2:
BF=2BE
=>EF=BE
=>EF=2ED
=>D là trung điểm của EF
Xét ΔFEC có
CD,EK là trung tuyến
CD cắt EK tại G
=>G là trọng tâm
b: G là trọng tâm của ΔFEC
=>GE/GK=1/2 và GC/DC=2

a: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
Do đó: ΔABD=ΔECD

a: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
Do đó: ΔABD=ΔECD

a: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
Do đó: ΔABD=ΔECD

\(a,ABM=MBC=\frac{ABC}{2}\)(BM là p/g t/g ABC)
\(ACN=NCB=\frac{ACB}{2}\)(CN là p/g t/g ABC)
mà ABC= ACB(t/g ABC cân A)
\(\rightarrow ABM=ACN\)
Xét t/g ABM và t/g ACN
Có ^BAC chung
AC= AB(t/g ABC cân A)
^ABM= ^ACN(cmt)
\(\rightarrow\)t/g ABM = t/g ACN(gcg)
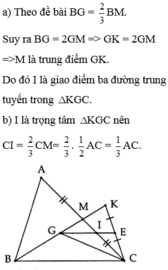
a: Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot15=10\left(cm\right)\)
b: Xét ΔABM và ΔCEM có
MA=MC
\(\widehat{AMB}=\widehat{CME}\)(hai góc đối đỉnh)
MB=ME
Do đó: ΔMAB=ΔMCE
=>\(\widehat{MAB}=\widehat{MCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BA//CE
d: Xét ΔNBF và ΔNAC có
\(\widehat{NBF}=\widehat{NAC}\)(BF//AC)
NB=NA
\(\widehat{BNF}=\widehat{ANC}\)(hai góc đối đỉnh)
Do đó: ΔNBF=ΔNAC
=>NF=NC
Xét ΔNAF và ΔNBC có
NA=NB
\(\widehat{ANF}=\widehat{BNC}\)(hai góc đối đỉnh)
NF=NC
Do đó: ΔNAF=ΔNBC
=>AF=BC
ΔNAF=ΔNBC
=>\(\widehat{NAF}=\widehat{NBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
Xét ΔMAE và ΔMCB có
MA=MC
\(\widehat{AME}=\widehat{CMB}\)(hai góc đối đỉnh)
ME=MB
Do đó: ΔMAE=ΔMCB
=>AE=CB
ΔMAE=ΔMCB
=>\(\widehat{MAE}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF(=BC)
nên A là trung điểm của EF