sin211 + sin220 + sin230 + sin240 + sin250 + sin260 + sin270 + sin280 = ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) sin230 độ - sin240 độ - sin250 độ + sin2 60 độ
= cos260o - cos250o - sin250o + sin260o
= (cos260o + sin260o) - (cos250o + sin250o)
= 1 - 1 = 0
b) cos225 độ - cos235độ + cos245 độ -cos2 55 độ + cos2 65 độ
= sin265o - sin255o + cos245o - cos255o + cos265o
= (sin265o + cos265o) - (sin255o + cos255o) + cos245o
= 1 - 1 +1/2
= 1/2

Chọn B.
Ta có: A = sin220 + sin240 + sin2 60 +…+ sin2840 + sin2860 + sin2880
A = ( sin220 + sin2 880) + ( sin2 40 + sin2860) +...+ (sin2440 + sin2460)
A = ( sin220 + cos220) + ( sin2 40 +…+ cos240) +...+ ( sin2440 + cos2440) ( do 2 góc phụ nhau sin góc này bằng cos góc kia).
A = 1 + 1 + 1 + ... + 1 = 22

Ta có:
![]()
![]()
Nên A = ( sin 2 1 0 + sin 2 89 0 ) + ( sin 2 2 0 + sin 2 88 0 ) +… + ( sin 2 44 0 + sin 2 46 0 ) + sin 2 45 0 + sin 2 90 0
= ( sin 2 1 0 + c o s 2 1 0 ) + ( sin 2 2 0 + c o s 2 2 0 ) + … + ( sin 2 44 0 + c o s 2 44 0 ) + sin 2 45 0 + sin 2 45 0
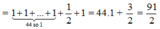
Vậy A = 91 2
Đáp án cần chọn là: C

Chọn B.
Ta có: A= ( sin230 + sin2870) + ( sin2750 + sin2150)
A= (sin230 + cos230) + ( sin2150 + cos2150)
= 1 + 1 = 2

\(=\dfrac{1}{cos\left(180+110\right)}+\dfrac{1}{\sqrt{3}sin\left(360-110\right)}\)
\(=-\dfrac{1}{cos110}-\dfrac{1}{\sqrt{3}sin110}\)
\(=\dfrac{-\sqrt{3}sin110-cos110}{\sqrt{3}\cdot sin110\cdot cos110}\)
\(=\dfrac{-2\left(\dfrac{\sqrt{3}}{2}\cdot sin110+\dfrac{1}{2}\cdot cos110\right)}{\dfrac{\sqrt{3}}{2}\cdot sin220}\)
\(=\dfrac{-2\cdot sin\left(110+30\right)}{\dfrac{\sqrt{3}}{2}\cdot sin220}=\dfrac{-2\cdot sin140}{\dfrac{\sqrt{3}}{2}\cdot sin220}\)

a) \(\sin220^0< \sin10^0< \sin40^0< \sin90^0\)
b) \(\cos138^0< \cos90^0< \cos15^0< \cos0^0\)

a)
\(\cos225^0=\cos\left(180^0+45^0\right)=-\cos45^0=-\dfrac{\sqrt{2}}{2}\)
\(\sin240^0=\sin\left(180^0+60^0\right)=-\sin60^0=-\dfrac{\sqrt{3}}{2}\)
\(\cos\left(-15^0\right)=-\cot15^0=-\tan75^0=-\tan\left(30^0+45^0\right)\)
\(=\dfrac{-\tan30^0-\tan45^0}{1-\tan30^0\tan45^0}=\dfrac{-\dfrac{1}{\sqrt{3}}-1}{1-\dfrac{1}{\sqrt{3}}}=-\dfrac{\sqrt{3}+1}{\sqrt{3}-1}\)
\(=-\dfrac{\left(\sqrt{3}+1\right)^2}{2}=-2-\sqrt{3}\)
\(\tan75^0=\cot15^0=2+\sqrt{3}\)
b)
\(\sin\dfrac{7\pi}{12}=\sin\left(\dfrac{\pi}{3}+\dfrac{\pi}{4}\right)=\sin\dfrac{\pi}{3}\cos\dfrac{\pi}{4}+\cos\dfrac{\pi}{3}\sin\dfrac{\pi}{4}\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\right)=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(\cos\left(-\dfrac{\pi}{12}\right)=\cos\left(\dfrac{\pi}{4}-\dfrac{\pi}{3}\right)=\cos\dfrac{\pi}{4}\cos\dfrac{\pi}{3}+\sin\dfrac{\pi}{3}\sin\dfrac{\pi}{4}\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\right)=0,9659\dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\right)=0,9659\)
\(\tan\dfrac{13\pi}{12}=\tan\left(\pi+\dfrac{\pi}{12}\right)=\tan\dfrac{\pi}{12}=\tan\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)\)
\(=\dfrac{\tan\dfrac{\pi}{3}-\tan\dfrac{\pi}{4}}{1+\tan\dfrac{\pi}{3}\tan\dfrac{\pi}{4}}=\dfrac{\sqrt{3}-1}{1+\sqrt{3}}=2-\sqrt{3}\)
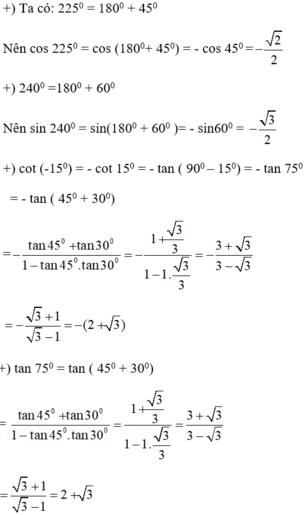
Áp dụng: \(\sin a=\cos\left(90-a\right);\text{ }\sin^2a+\cos^2a=1\Rightarrow\sin^2a+\sin^2\left(90-a\right)=1\)
\(\sin^210+\sin^220+...+\sin^280=\left(\sin^210+\sin^280\right)+\left(\sin^220+\sin^270\right)+...+\left(\sin^240+\sin^250\right)\)
\(=1+1+1+1=4\)