Cho tam giác ABC vuông tại A ,Có góc B = 50 độ
a.Tính số đo góc c và so sánh AB và AC
b. Cho CM phân giác góc ACB ,lấy E thuộc BC,sao cho CA = CE.Chứng minh tam giác ACM=tam giác ECM
c.Chứng minh CM vuoogn góc AE và góc MAE = góc MEA
d.Kẻ EM cắt AC tại Q .Chứng minh QB song song AE.
Có vẽ hình

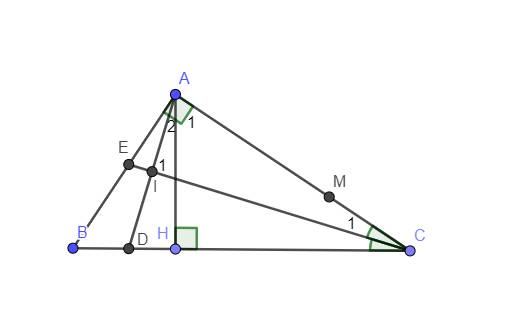
a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=40^0\)
Xét ΔABC có \(\widehat{ABC}>\widehat{ACB}\)
mà AC,AB lần lượt là cạnh đối diện của các góc ABC,ACB
nên AC>AB
b: Xét ΔCAM và ΔCEM có
CA=CE
\(\widehat{ACM}=\widehat{ECM}\)
CM chung
Do đó: ΔCAM=ΔCEM
c: Ta có: ΔCAM=ΔCEM
=>MA=ME
=>M nằm trên đường trung trực của AE(1)
ta có: CA=CE
=>C nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra CM là đường trung trực của AE
=>CM\(\perp\)AE tại trung điểm của AE
Xét ΔMAE có MA=ME
nên ΔMAE cân tại M
=>\(\widehat{MAE}=\widehat{MEA}\)
d: Xét ΔCEQ vuông tại E và ΔCAB vuông tại A có
CE=CA
\(\widehat{ECQ}\) chung
Do đó: ΔCEQ=ΔCAB
=>CQ=CB
Xét ΔCQB có \(\dfrac{CA}{CQ}=\dfrac{CE}{CB}\)
nên AE//QB