1) a) Cho \(\Delta ABC\) cân tại A, \(\widehat{B}=75^o37'19''.\) Gọi I là trung điểm của AB. Tính \(\widehat{ACI}\) = ?
b) Cho \(\Delta ABC\) có AC=35cm, \(\widehat{B}=60^o\) , \(\widehat{C}=50^o\) . Tính chu vi , diện tích \(\Delta ABC\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(K đăng hình đc nên hình tự vẽ)
Kẻ \(AH\perp BC\left(H\in BC\right)\)
• Xét \(\Delta HAC\) vuông tại \(H\) có
\(\sin C=\dfrac{AH}{AC}\Rightarrow AH=\sin50^o.35\approx26,81\left(cm\right)\)
\(\cos C=\dfrac{HC}{AC}\Rightarrow HC=\cos50^o.35\approx22,5\left(cm\right)\)
• Xét \(\Delta HAB\) vuông tại \(H\) có
\(\tan B=\dfrac{AH}{BH}\Rightarrow BH\approx\dfrac{26,81}{\tan60^o}\approx15,48\left(cm\right)\)
\(\cos B=\dfrac{AH}{AB}\Rightarrow AB\approx\dfrac{26,81}{\cos60^o}\approx53,62\left(cm\right)\)
*Khi đó chu vi \(\Delta ABC\) bằng \(AB+BC+AC\)
\(\approx53,62+\left(22,5+15,48\right)+35\)
\(\approx192,48\left(cm\right)\)
*Khi đó \(S_{\Delta ABC}=\dfrac{AH.BC}{2}\approx\dfrac{26,81.\left(22,5+15,48\right)}{2}\approx509,12\left(cm^2\right)\)
#F.C

Do ΔABC cân tại B => A = C = \(\dfrac{180^o-80^o}{2}=50^o\)
=> góc BAI = 50o - 10o = 40o
góc BCI = 50o - 30o = 20o
=> \(IBC=\dfrac{1}{3}ABI\Rightarrow IBC=\dfrac{80^o}{3+1}=20^o;ABI=80^o-20^o=60^o\)
\(\Leftrightarrow AIB=180^o-40^o-60^o=80^o\)

Bài 4:
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{ABE}=\widehat{ACD}\)
BE=CD
Do đó: ΔABE=ΔACD
Suy ra: \(\widehat{EAB}=\widehat{DAC}\)
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Ta có: ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xét ΔDAE cân tại A có \(\widehat{DAE}=60^0\)
nên ΔDAE đều
Nhận xét: Các góc trong ΔAED bằng nhau và cùng bằng 60 độ

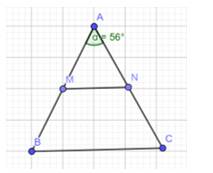
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC