a) ta có  \(\frac{y1}{x1}=\frac{y2}{x2}=\frac{y1+y2}{x1+x2}=\frac{3k}{4k}=\frac{3}{4}\)

=>\(y=\frac{3}{4}.x;và:x=\frac{4}{3}y\)

b) y₁ +x₂ =5 

x1+x2 = 16  ; x1 = 4/3 y1  => 4/3y1 + x2 =16  => 1/3y1 +(y1+x2) =16 => 1/3 y1 +5 =16 => 1/3 y1 =11 => y1 =33

=> x1 =4/3 y1 =4/3 .33 =44

Lời giải:

** Sửa lại hàm số: $y=-x+3$

a. Bạn có thể tự vẽ.

b. Để $y=(2k-1)x+1$ song song với (d)$ thì:

$2k-1=-1$

$\Leftrightarrow k=0$

c. PT hoành độ giao điểm của $(d)$ và $y=(k-3)x+5$:

$-x+3=(k-3)x+5$

$\Leftrightarrow (k-2)x=-2$

$\Leftrightarrow x=\frac{-2}{k-2}$ (đk: $k\neq 2$)

Khi đó: $y=-x+3=\frac{2}{k-2}+3$

Hai đths cắt nhau tại điểm có tung độ $7$

$\Leftrightarrow \frac{2}{k-2}+3=7$

$\Leftrightarrow \frac{2}{k-2}=4$

$\Leftrightarrow k-2=\frac{1}{2}\Leftrightarrow k=2,5$

a: Sửa đề: y=-x+3

Vẽ đồ thị

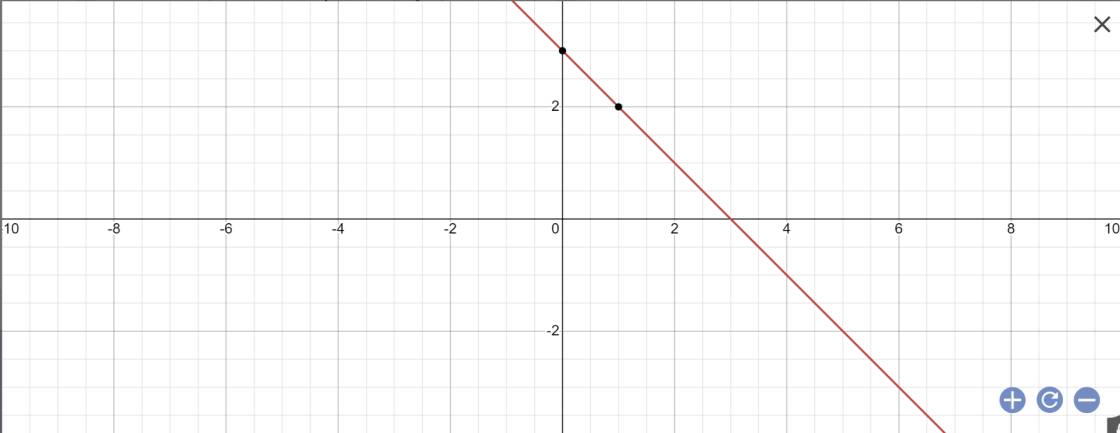
b: Để đường thẳng y=(2k-1)x+1 song song với (d) thì 

\(\left\{{}\begin{matrix}2k-1=-1\\1\ne3\left(đúng\right)\end{matrix}\right.\)

=>2k-1=-1

=>2k=0

=>k=0

c: Thay y=7 vào y=-x+3, ta được:

-x+3=7

=>-x=4

=>x=-2

Thay x=-2 và y=7 vào y=(k-3)x+5, ta được:

-2(k-3)+5=7

=>-2(k-3)=2

=>k-3=-1

=>k=2

A, B thuộc (P), (d) ?

Phương trình hoành độ giao điểm của (P) và (d) là:

\(x^2=k\left(x-1\right)+2\Leftrightarrow x^2-kx+\left(k-2\right)=0\).

Ta có \(\Delta=k^2-4\left(k-2\right)=\left(k-2\right)^2+2>0\forall k\) nên phương trình trên luôn có hai nghiệm phân biệt.

Theo hệ thức Viète ta có \(\left\{{}\begin{matrix}x_1x_2=k-2\\x_1+x_2=k\end{matrix}\right.\).

Ta có \(x_1^2+y_1+x_2^2+y_2=14\)

\(\Leftrightarrow2x_1^2+2x_2^2=14\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=7\)

\(\Leftrightarrow k^2-2\left(k-2\right)=7\Leftrightarrow k^2-2k-3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}k=-1\\k=3\end{matrix}\right.\).

Vậy...

Bạn tham khảo:

https://hoc24.vn/hoi-dap/question/916292.html

\(\left\{{}\begin{matrix}x+y=2k-1\\\left(x+y\right)^2-2xy=2k^2+4k-11\end{matrix}\right.\)

\(\Rightarrow2xy=\left(2k-1\right)^2-\left(2k^2+4k-11\right)=2k^2-8k+12\)

\(\Rightarrow xy=k^2-4k+6=\left(k-2\right)^2+2\ge2\)

Dấu "=" xảy ra khi \(k=2\)

+, Nếu x = 2 => 2^2-2y^2 = 1

=> 2y^2 = 4-1-3

=> ko tồn tại y

+, Nếu x > 2 => x lẻ 

=> x^2 là số chính phương lẻ => x^2 chia 8 dư 1

=> 2y^2 = x^2-1 chia hết cho 8

=> y^2 chia hết cho 4

=> y chia hết cho 2 

=> y=2 ( vì y là số nguyên tố )

=> x^2-2.2^2 =1

=> x^2-8=1

=> x^2=1+8=9

=> x=3 ( vì x là số nguyên tố )

Vậy x=3 và y=2

Tk mk nha

tại sao lại có x=2

PTHĐGĐ là:

x^2-(2m+1)x+2m=0

Δ=(2m+1)^2-4*2m

=4m^2+4m+1-8m=(2m-1)^2

Để (P) cắt (d) tại hai điểm phân biệt thì 2m-1<>0

=>m<>1/2

y1+y2-x1x2=1

=>(x1+x2)^2-3x1x2=1

=>(2m+1)^2-3*2m=1

=>4m^2+4m+1-6m-1=0

=>4m^2-2m=0

=>m=0 hoặc m=1/2(loại)

tik mik nha mik tik lại

câu hỏi này mik chưa học đến vì mik mới học lớp 6 thui

tham khảo chtt nha bạn

chứ câu này mk chưa có học