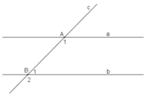
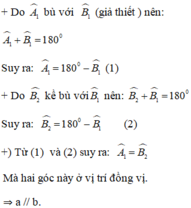Chứng minh rằng :Nếu hai đường thẳng cắt một đường thẳng mà trong những góc tạo thành có một cặp góc trong cùng phía bù nhau thì hai đường thẳng đó song song với nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ý bn đấy là chứng minh cái ddingj lý đấy ra nha bn Vũ Hải Anh

Theo định lí Pi-ta-go
Trong 1 cặp góc trong cùng phía bù nhau(900) thì 2 đường thằng đó song song với nhau
Trần Thị Vân Ngọc bn chỉ cần áp dụng định lý Pi-ta-go vào bài này như bn Vương Nguyễn đã nói nhé

| gt | hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc trong cùng phía bù nhau |
| kl | a // b |
Cm: theo gt ta có : góc A1 + góc B1 = 180 độ
lại có góc A1 + góc A2 = 180 độ( hai góc kề bù)
=> góc A1 = góc B2
mà hai góc này ở vị trí hai góc đồng vị
=> a // b
mình sửa câu trả lời vừa nãy một chút.
phần cm:
=> góc B1 = góc A2

Chứng minh định lí
A1 + B1 = 1800
Mà A1 + A2 = 1800 ( 2 góc kề bù )
\(\Rightarrow\)B1 = A2
Mà B1 và A2 là 2 góc đồng vị
\(\Rightarrow\)a // b
GT:Nếu hai đg thẳng a,b cất đg thảng c.............bù nhau
KL:Thì a và b song song với nhau

CM:
\(\widehat{B2}+\widehat{A1}=180^0\) (1)
\(\widehat{B1}+\widehat{B2}=180^0\) ( 2 góc kề bù ) (2)
Từ (1) và (2)
\(\Rightarrow\widehat{B2}+\widehat{A1}=\widehat{B1}+\widehat{B2}\)
\(\Rightarrow\widehat{A1}=\widehat{B1}\) mà 2 góc này ở vị trí đồng vị
\(\Rightarrow a//b\)