Cho hình thang ABCD có đáy lớn CD. Trên CD lấy 2 điểm I,K sao cho AK//BC,BI//AD, BI cắt AC tại F, AK cắt BD tại E.CMR:
a) AB//EF
b) \(AB\le\frac{EF+CD}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì ABID và ABCK là hbh nên \(AB=DI;AB=CK\)
Do đó \(DI=CK\Rightarrow DI-KI=CK-KI\)
Vậy \(KD=CI\)
b, Áp dụng Talet: \(\dfrac{DE}{EB}=\dfrac{DK}{AB}=\dfrac{CI}{AB}=\dfrac{IF}{FB}\left(DK=CI\right)\)
Suy ra EF//CD (Talet đảo)
Áp dụng Talet: \(\dfrac{AB}{EF}=\dfrac{DI}{EF}=\dfrac{BD}{BE}=\dfrac{BE+ED}{BE}=1+\dfrac{ED}{BE}=1+\dfrac{DK}{AB}=1+\dfrac{CD-CK}{AB}=1+\dfrac{CD-AB}{AB}=\dfrac{CD}{AB}\)
Vậy \(AB^2=EF\cdot CD\)

toán hình lớp 8 đấy , chẳng qua bạn ấy học lớp 9 nên mới chọn toán lớp 9 thôi

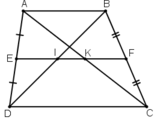
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm