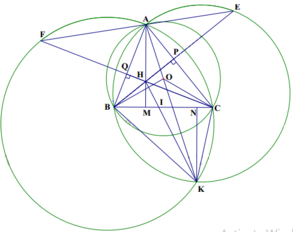
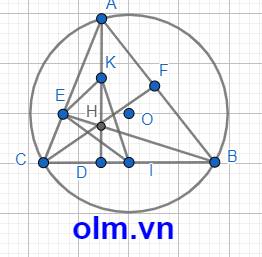
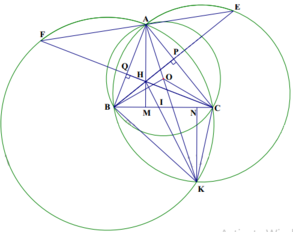
cho đường tròn (O) và dây BC cố định không đi qua tâm O. điểm A di động trên cung lớn BC sao cho tam giác ABC nhọn. các đường cao AD, BE và CF của tam giác ABC cắt nhau tại điểm H, gọi I là giao điểm của ADvaf EF.
1, chững minh CEHD là tứ giác nội tiếp
2, chững minh góc DEH = góc FEH và 1/DH +1/DA=2/DI

1: Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
nên CEHD là tứ giác nội tiếp
2: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
Ta có: \(\widehat{DEH}=\widehat{DCH}\)(CEHD nội tiếp)
\(\widehat{FEH}=\widehat{FAH}\)(AEHF nội tiếp)
mà \(\widehat{DCH}=\widehat{FAH}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{DEH}=\widehat{FEH}\)