Bài IV (3,0 điểm). Cho tam giác ABC nhọn (^ B < AC ) nội tiếp đường tròn (O). Các đường cao AD, BN, CM của tam giác ABC cắt nhau tại H.
1. Chứng minh bốn điểm B, M, N, C cùng thuộc một đường tròn.
2. Qua điểm N kẻ đường thẳng vuông góc với MN cắt MC tại điểm K. Chứng minh NK // AO.




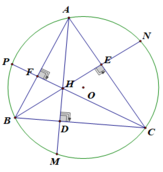

1: Xét tứ giác BMNC có \(\widehat{BMC}=\widehat{BNC}=90^0\)
nên BMNC là tứ giác nội tiếp
=>B,M,N,C cùng thuộc một đường tròn
2: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{ANM}\left(=180^0-\widehat{MNC}\right)\)
nên \(\widehat{xAC}=\widehat{ANM}\)
=>MN//Ax
mà Ax\(\perp\)AO
nên MN\(\perp\)AO
mà MN\(\perp\)NK
nên NK//AO
1: Xét tứ giác BMNC có 𝐵𝑀𝐶^=𝐵𝑁𝐶^=900BMC=BNC=900
nên BMNC là tứ giác nội tiếp
=>B,M,N,C cùng thuộc một đường tròn
2: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
𝑥𝐴𝐶^xAC là góc tạo bởi tiếp tuyến Ax và dây cung AC
𝐴𝐵𝐶^ABC là góc nội tiếp chắn cung AC
Do đó: 𝑥𝐴𝐶^=𝐴𝐵𝐶^xAC=ABC
mà 𝐴𝐵𝐶^=𝐴𝑁𝑀^(=1800−𝑀𝑁𝐶^)ABC=ANM(=1800−MNC)
nên 𝑥𝐴𝐶^=𝐴𝑁𝑀^xAC=ANM
=>MN//Ax
mà Ax⊥⊥AO
nên MN⊥⊥AO
mà MN⊥⊥NK
nên NK//AO