(Giải thích chi tiết tại sao)
Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây đúng?
A. A là tâm đường tròn ngoại tiếp tam giác ABC
B. A là trọng tâm tam giác ABC
C. A là trực tâm tam giác ABC
D. A là tâm đường tròn nội tiếp tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(SO\perp ABC\Rightarrow\) các tam giác SOA, SOB, SOC đều vuông tại O
Đặt \(SA=SB=SC=a\) , áp dụng Pitago:
\(OA=\sqrt{SA^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OB=\sqrt{SB^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OC=\sqrt{SC^2-SO^2}=\sqrt{a^2-SO^2}\)
\(\Rightarrow OA=OB=OC\Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác ABC

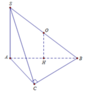
Đáp án D
Vì B C ⊥ S A B C ⊥ C A ⇒ B C ⊥ S A C ⇒ B C ⊥ S C ⇒ O là tâm đường tròn ngoại tiếp tam giác SBC
Vì S A ⊥ A B C ⇒ H là trung điểm của AB

* Do O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của 3đường trung trực của tam giác ABC.
Lại có: M là trung điểm của BC nên O M ⊥ B C (OM là 1 đường trung trực của tam giác) (1)
* Lại có H là trực tâm của tam giác ABC nên: A H ⊥ B C (2)
Từ (1) và (2) suy ra: OM // AH.
* Nếu tam giác ABC nhọn thì O nằm trong tam giác ABC nên A H → , O M → cùng hướng
* Nếu tam giác ABC tù thì O nằm ngoài tam giác ABC nên A H → , O M → ngược hướng.
Đáp án A

a)
– Tọa độ trọng tâm G của tam giác ABC là:
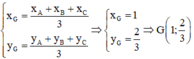
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 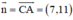 là một vtpt
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 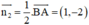 là một vtpt
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
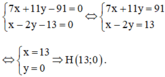
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
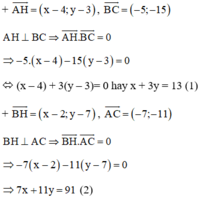
Từ (1) và (2) ta có hệ phương trình
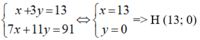
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
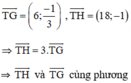
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
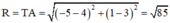
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85

a: Vì góc A nhọn nên chắc chắn tam giác ABC không thể vuông cân
=> Loại
b: Gọi giao điểm của BH và AC là K
=> BK\(\perp\)AC tại K
Ta có: ΔABK vuông tại K
nên \(\widehat{ABK}+\widehat{BAK}=90^0\)
hay \(\widehat{BAC}=60^0\)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)
nên ΔABC đều

a: \(\overrightarrow{AB}=\left(-3;4\right)\)
\(\overrightarrow{AC}=\left(8;6\right)\)
Vì \(\overrightarrow{AB}\cdot\overrightarrow{AC}=0\) nên ΔABC vuông tại A
c: Tọa độ trọng tâm G là:
\(\left\{{}\begin{matrix}x_G=\dfrac{1-2+9}{3}=\dfrac{8}{3}\\y_G=\dfrac{2+6+8}{3}=\dfrac{16}{3}\end{matrix}\right.\)
A là trực tâm của tam giác ABC vì A là giao của 2 đường cao AB và AC
Chọn C
Xét ΔABC có
AC là đường cao ứng với cạnh AB
AB là đường cao ứng với cạnh AC
AC cắt AB tại A
Do đó: A là trực tâm của ΔABC