Bài 3. Cho tam giác MNP cân tại M. Lấy điểm D trên cạnh MN, điểm E trên cạnh MP sao cho
ND = PE.
a) Chứng minh:ΔNDP = ΔPEN.
b) Chứng minh:ΔMDP = ΔMEN.
c) Gọi K là giao điểm của NE và DP. Chứng minh: ΔKNP cân tại K.
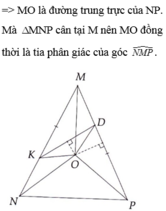
d) Chứng minh: MK là tia phân giác của góc NMP.
e) Lấy H là trung điểm của NP. Chứng minh: M, K, H là 3 điểm thẳng hàng.
f) Chứng minh: DE // NP


a: Xét ΔDNP và ΔEPN có
DN=EP
\(\widehat{DNP}=\widehat{EPN}\)
NP chung
Do đó: ΔDNP=ΔEPN
b: ΔDNP=ΔEPN
=>DP=EN
Ta có: MD+DN=MN
ME+EP=MP
mà DN=EP và MN=MP
nên MD=ME
Xét ΔMEN và ΔMDP có
ME=MD
EN=DP
MN=MP
Do đó: ΔMEN=ΔMDP
c: Ta có: ΔDNP=ΔEPN
=>\(\widehat{DPN}=\widehat{ENP}\)
=>\(\widehat{KNP}=\widehat{KPN}\)
=>ΔKNP cân tại K
d: Xét ΔMNK và ΔMPK có
MN=MP
NK=PK
MK chung
Do đó: ΔMNK=ΔMPK
=>\(\widehat{NMK}=\widehat{PMK}\)
=>MK là phân giác của góc NMP
e: Ta có: ΔMNP cân tại M
mà MH là đường trung tuyến
nên MH là phân giác của góc NMP
mà MK là phân giác của góc NMP
nên M,H,K thẳng hàng
f: Xét ΔMNP có \(\dfrac{MD}{MN}=\dfrac{ME}{MP}\)
nên DE//NP