Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α. Biết tanα = 5/12. Hãy tính :
a) Độ dài cạnh AC
b) Độ dài cạnh BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

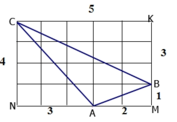
Gọi mỗi góccòn lại trên giấy ô vuông là K; M; N
Xét Tg AMB vuông tại M ta có:
AB^2 = AM^2 + MB^2 (định lí Pi-ta-go)
Thay số: AB^2 = 22 + 12 = 5
=> AB = căn 5
Xét Tg ANC vuông tại N ta có:
AC^2 = AN^2 + NC^2 (định lí Pi-ta-go )
AC^2= 32 + 42 = 25
=> AC = 5
Xét Tg BKC vuông tại K ta có:
BC^2= BK^2+ KC^2(định lí Pi-ta-go )
BC^2 = 32 + 52 = 34
=>BC= căn 34

diện tích tam giác ABC là
\(\left(12,7\times15,6\right)\div2=99,06\left(cm^2\right)\)
đáp số : \(99,06cm^2\)
Diện tích hình tam giác vuông abc là :
15.6 x 12.7 : 2 = 99.06 ( cm2 )
Đáp số : 99.08 cm2

Bài 3:
Gọi độ dài hai cạnh góc vuông lần lượt là a,b
Theo đề, ta có: a/8=b/15
Đặt a/8=b/15=k
=>a=8k; b=15k
Ta có: \(a^2+b^2=51^2\)
\(\Leftrightarrow289k^2=2601\)
=>k=3
=>a=24; b=45
Bài 6:
Xét ΔABC có \(10^2=8^2+6^2\)
nên ΔABC vuông tại A
Refer:
2,
Ta có:AH là đường cao ΔABC
⇒AH ⊥ BC tại H
⇒∠AHB=∠AHC=90°
⇒ΔAHB và ΔAHC là Δvuông H
Xét ΔAHB vuông H có:
AH² + HB²=AB²(Py)
⇔24² + HB²=25²
⇔ HB²=25² - 24²
⇔ HB²=49
⇒ HB=7(đvđd)
Chứng minh tương tự:HC=10(đvđd)
Ta có:BC=BH + CH=7 + 10=17(đvđd)

Độ dài cạnh AB so với cạnh BC là: \(\dfrac{3}{4}\)x \(\dfrac{4}{5}\) =\(\dfrac{3}{5}\)
Độ dài cạnh AB là: 72:(3+4+5)x3= 18(cm)
Độ dài cạnh AC là: 72:(3+4+5)x4 = 24(cm)
Diện tích tam giác ABC là: 18x24:2 = 216(\(cm^2\))
Đáp số: 216cm2

Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
⇒ AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
⇒ AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
⇒ BC = √34

Lời giải:
Coi độ dài cạnh AB là 3 phần thì độ dài cạnh AC là 4 phần, độ dài cạnh BC là 5 phần.
Tổng số phần bằng nhau: $3+4+5=12$ (phần)
Độ dài cạnh AB: $144:12\times 3=36$ (cm)
Độ dài cạnh AC: $144:12\times 4=48$ (cm)
Diện tích tam giác $ABC$: $36\times 48:2=864$ (cm2)
Tam giác ABC vuông tại A ta có:
\(tanB=\dfrac{AC}{AB}=>\dfrac{5}{12}=\dfrac{AC}{6}=>AC=\dfrac{5\cdot6}{12}=\dfrac{5}{2}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\\ =>BC=\sqrt{AB^2+AC^2}\\ =>BC=\sqrt{6^2+\left(\dfrac{5}{2}\right)^2}=\dfrac{13}{2}\left(cm\right)\)
Để giải bài toán, ta cần sử dụng một số công thức và định lý trong hình học, đặc biệt là định lý Pythagore và định nghĩa của các hàm số lượng giác.
Cho tam giác ABC vuông tại A, với AB = 6 cm và tanα = 5/12. Góc B = α.
a) Tính độ dài cạnh AC
Vì tam giác vuông tại A, góc α là góc B, ta có:
tan(α)=đoˆˊi diệnkeˆˋ\tan(\alpha) = \frac{\text{đối diện}}{\text{kề}}tan(α)=keˆˋđoˆˊi diện
Trong tam giác ABC vuông tại A:
tan(α)=BCAC\tan(\alpha) = \frac{BC}{AC}tan(α)=ACBC
Theo đề bài, tan(α)=512\tan(\alpha) = \frac{5}{12}tan(α)=125.
Do đó, ta có:
BCAC=512\frac{BC}{AC} = \frac{5}{12}ACBC=125
Từ đó suy ra:
BC=512ACBC = \frac{5}{12} ACBC=125AC
b) Tính độ dài cạnh BC
Ta sử dụng định lý Pythagore cho tam giác ABC vuông tại A:
BC2=AB2+AC2BC^2 = AB^2 + AC^2BC2=AB2+AC2
Đầu tiên, ta cần tính AC.
Biết rằng tan(α)=512\tan(\alpha) = \frac{5}{12}tan(α)=125, do đó ta có:
sin(α)=BCBC2+AC2\sin(\alpha) = \frac{BC}{BC^2 + AC^2}sin(α)=BC2+AC2BC sin(α)=BCBC2+AC2\sin(\alpha) = \frac{BC}{BC^2 + AC^2}sin(α)=BC2+AC2BC
Vì tan(α) = 5/12 nên ta đặt BC = 5k và AC = 12k. Vì thế:
BC=5kBC = 5kBC=5k
AC=12kAC = 12kAC=12k
Sử dụng định lý Pythagore:
BC2=AB2+AC2BC^2 = AB^2 + AC^2BC2=AB2+AC2
(5k)2=AB2+(12k)2(5k)^2 = AB^2 + (12k)^2(5k)2=AB2+(12k)2
25k2=62+144k225k^2 = 6^2 + 144k^225k2=62+144k2
25k2=36+144k225k^2 = 36 + 144k^225k2=36+144k2
Từ đó, ta có:
AC=12k5AC = \frac{12k}{5}AC=512k
AC2=AB2+BC2AC^2 = AB^2 + BC^2AC2=AB2+BC2
(12k)2=62+(5k)2(12k)^2 = 6^2 + (5k)^2(12k)2=62+(5k)2
144k2=36+25k2144k^2 = 36 + 25k^2144k2=36+25k2
144k2−25k2=36144k^2 - 25k^2 = 36144k2−25k2=36
119k2=36119k^2 = 36119k2=36
k2=36119k^2 = \frac{36}{119}k2=11936
k=36119k = \sqrt{\frac{36}{119}}k=11936
k=6119k = \frac{6}{\sqrt{119}}k=1196
BC=5k=5×6119=30119BC = 5k = 5 \times \frac{6}{\sqrt{119}} = \frac{30}{\sqrt{119}}BC=5k=5×1196=11930
AC=12k=12×6119=72119AC = 12k = 12 \times \frac{6}{\sqrt{119}} = \frac{72}{\sqrt{119}}AC=12k=12×1196=11972
Chúng ta có thể tính toán lại bằng cách:
Suy ra: BC=512ACBC = \frac{5}{12} ACBC=125AC AC=12×65=14.4AC = \frac{12 \times 6}{5} = 14.4AC=512×6=14.4 BC=5×1.2=6BC = 5 \times 1.2 = 6BC=5×1.2=6
Suy ra:...