a) Xét tứ giác BFEC có 

\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)

nên BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Xét ΔAEB vuông tại E và ΔAFC vuông tại F có 

\(\widehat{BAE}\) chung

Do đó: ΔAEB\(\sim\)ΔAFC(g-g)

Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)

hay \(AE\cdot AC=AB\cdot AF\)

1: góc AFB=góc AEB=góc ADB=90 độ

=>A,F,B,E,D cùng nằm trên 1 đường tròn

2: Xét ΔAFE và ΔACM có

góc FAE chung

góc AFE=góc ABE=góc ADE=góc MCA

=>ΔAFE đồng dạng với ΔACM

=>AE/AM=AF/AC

=>AM/AC=AE/AF

góc FAB=góc ACB

=>góc FBA=90 độ-góc ACB=góc EBC

Vẽ các đường trung tuyến AM và BK cắt nhau tại G

Gọi I là giao đường trung trực IK và IM

Mik chỉ viết gợi ý chứng minh thôi nha

1) CM tam giác AHB đồng dạng tam giác MIK

2) CM tam giác HAG đồng dạng IMG

3) CM được H,G,I thằng hàng bằng cách CM góc HGI=180 độ. Cm bằng những góc tương ứng của các cặp tam giác đồng dạng

Tham khảo:

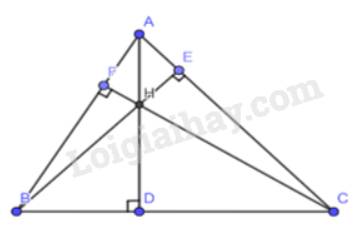
+) Xét tam giác HBC ta có :

HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC

BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC

CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC

Ta kéo dài HD, BF, CE sẽ cắt nhau tại A

\( \Rightarrow \) A là trực tâm tam giác HBC

+) Xét tam giác HAB ta có :

HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB

BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB

BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB

Ta kéo dài HF, BD, AE sẽ cắt nhau tại C

\( \Rightarrow \) C là trực tâm tam giác HAB

+) Xét tam giác HAC ta có :

HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC

AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC

CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC

Ta kéo dài CD, HE, AF sẽ cắt nhau tại B

\( \Rightarrow \) B là trực tâm tam giác HAC.

Ta cần chứng minh H là trực tâm của tam giác ASM. Với mục đích này, ta sẽ sử dụng tính chất của hình chữ nhật.

Vì M là trung điểm BC, ta có BM = MC. Do đó, SM là đường trung trực của BC.

Vì EF ⊥ BE và CF, nên EF song song với đường BC (vì BE // CF). Do đó, S nằm trên đường trung trực của BC.

Vì H là giao điểm của AD và BE, ta có AH  ⊥ BC và BH ⊥ AC. Do đó, AH // SM và BH // SM.

Khi đó, ta suy ra được rằng tứ giác ABSH là hình chữ nhật (do có 2 cặp cạnh đối nhau là song song và bằng nhau).

Do AS là đường chéo của hình chữ nhật ABSH, nên H là trực tâm của tam giác ASM.

Vậy, H là trực tâm của tam giác ASM. 

Bạn nhầm đề không vậy:), s là giao điểm cả ef và bc mà suy ra được s là trung trực của bc dc hả?:) nhân tài đất Việt đây rồi !! 🤣🤣🤣🤣🤣

\({}\)

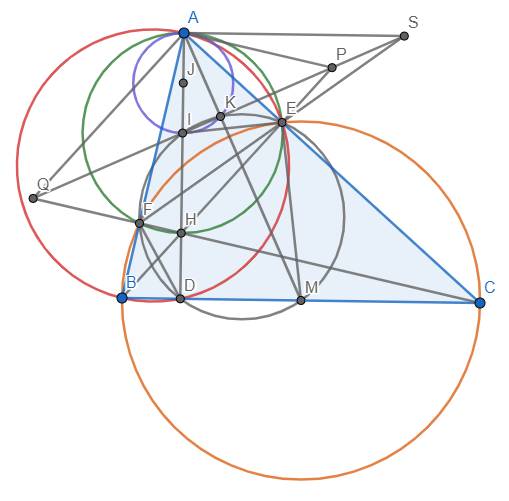
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.

Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\) 

\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)

\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))

Vậy \(IE\perp ME\)

b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)

 Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).

c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP

\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)

\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)

\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)

\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)

Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)