Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
*Hình vuông:
#include <bits/stdc++.h>
using namespace std;
double n;
int main()
{
cin>>n;
cout<<fixed<<setprecision(2)<<n*4<<endl;
cout<<fixed<<setprecision(2)<<n*n;
return 0;
}
6 cm2 ? Ko chắc.cách làm tra mạng nha,mk lười chép lắm!
Bài 2:
(Bạn vẽ hình thì vẽ nửa trên đường thôi nha, tại đề cho là nửa đường tròn tâm O)
a, Vì AC//BD (⊥AB) nên ABDC là hthang
Mà \(\widehat{CAB}=90^0\) nên ABDC là hthang vuông
b, Gọi I là trung điểm CD
Mà O là trung điểm AB nên OI là đtb hthang ABDC
Do đó OI//AC\(\Rightarrow\)OI⊥AB
Mà tam giác OCD vuông tại O nên OI là bán kính đg tròn ngoại tiếp tam giác OCD
Do đó AB là tiếp tuyến tại O của (I)
Vậy đường tròn ngoại tiếp tam giác COD tiếp xúc với đường thẳng AB tại O.
c, Kẻ OH⊥CD
Vì \(\widehat{AOC}=\widehat{IOD}\) (cùng phụ \(\widehat{COI}\)), \(\widehat{IOD}=\widehat{IDO}\left(IO=ID=\dfrac{1}{2}CD\right)\) nên \(\widehat{AOC}=\widehat{IDO}\Rightarrow90^0-\widehat{AOC}=90^0-\widehat{IDO}\Rightarrow\widehat{ACO}=\widehat{HCO}\)
Vì \(\left\{{}\begin{matrix}\widehat{ACO}=\widehat{HCO}\\CO.chung\\\widehat{CAO}=\widehat{CHO}=90^0\end{matrix}\right.\) nên \(\Delta AOC=\Delta HOC\Rightarrow OA=OH\Rightarrow H\in\left(O\right)\)
Mà CD⊥OH nên CD là tt tại H của (O)
Do đó \(CA\cdot DB=CH\cdot HD=OH^2=R^2\) (kết hợp HTL)
Vào đây Câu hỏi của Nguyễn Đình Thi - Toán lớp 9 - Học toán với OnlineMath
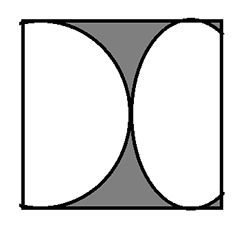
a: Xét (O) có
ΔCMD nội tiếp
CD là đường kính
Do đó:ΔCMD vuông tại M
=>DM\(\perp\)CF tại M
b: Xét (O) có AB,CD là các đường kính và AB\(\perp\)CD tại O
nên \(sđ\stackrel\frown{CA}=sđ\stackrel\frown{CB}=sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD}\)
Xét (O) có \(\widehat{MNB}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung MB,AD
=>\(\widehat{MNB}=\dfrac{1}{2}\left(sđ\stackrel\frown{MB}+sđ\stackrel\frown{AD}\right)=\dfrac{1}{2}\left(sđ\stackrel\frown{MB}+sđ\stackrel\frown{BD}\right)=\dfrac{1}{2}\cdot sđ\stackrel\frown{MD}\)
Xét (O) có
\(\widehat{DME}\) là góc tạo bởi tiếp tuyến ME và dây cung MD
=>\(\widehat{DME}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MD}\)
=>\(\widehat{DME}=\widehat{MNB}\)
=>ΔENM cân tại E
Ta có: \(\widehat{EMN}+\widehat{EMF}=\widehat{FMN}=90^0\)
\(\widehat{ENM}+\widehat{EFM}=90^0\)(ΔNMF vuông tại M)
mà \(\widehat{ENM}=\widehat{EMN}\)
nên \(\widehat{EMF}=\widehat{EFM}\)
=>ΔEFM cân tại E