xy+3x-2y-7=0

 =>(xy-2y)+3x-7=0

=>y(x-2)+3x-6=-1

=>y(x-2)+3(x-2)=-1

=>(y+3)(x-2)=-1

=>y+3 và x-2 thuộc Ư(1)={1;-1}

Xét y+3=1 =>y=2 <=>x-2=-1 =>x=1

Xét y+3=-1 =>y=-4 <=>x-2=1 =>x=3

Cách 1

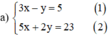
Từ (1) ta rút ra được y = 3x – 5 (*)

Thế (*) vào phương trình (2) ta được :

5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.

Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.

Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).

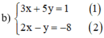
Từ (2) ta rút ra được y = 2x + 8 (*)

Thế (*) vào phương trình (1) ta được :

3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.

Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.

Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).

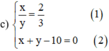
Từ (1) ta rút ra được x = 2 3 y  (*)

Thế (*) vào phương trình (2) ta được :

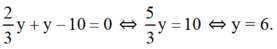
Thay y = 6 vào (*) ta được x = 4.

Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).

Cách 2

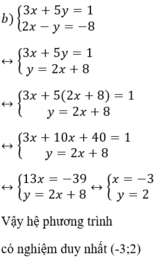
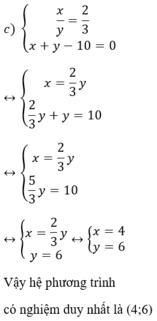
Kiến thức áp dụng

+ Giải hệ phương trình 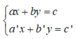 ta làm như sau:

Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).

Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .

Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.

+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.

\(\hept{\begin{cases}x^2+2xy+2y^2+3x=0\left(1\right)\\xy+y^2+3y+1=0\left(2\right)\end{cases}}\)

Lấy pt (1)+2*pt (2) ta được:

\(\left(x+2y\right)^2+3\left(x+2y\right)+2=0\)

\(\Leftrightarrow\left(x+2y+1\right)\left(x+2y+2\right)=0\)

• Nếu \(x+2y+1=0\Rightarrow x=-2y-1\)thay vào (2) ta được:

\(y^2-2y-1=0\)\(\Rightarrow\orbr{\begin{cases}y=1+\sqrt{2}\\y=1-\sqrt{2}\end{cases}}\Rightarrow\orbr{\begin{cases}x=-3-2\sqrt{2}\\x=-3+2\sqrt{2}\end{cases}}\)

• Nếu \(x+2y+2=0\Rightarrow x=-2y-2\) thay vào (2) ta được:

\(y^2-y-1=0\Rightarrow\orbr{\begin{cases}y=\frac{1-\sqrt{5}}{2}\\y=\frac{1+\sqrt{5}}{2}\end{cases}}\Rightarrow\orbr{\begin{cases}x=-3+\sqrt{5}\\x=-3-\sqrt{5}\end{cases}}\)

Vậy hpt có 4 nghiệm (x;y) là : \(\left(-3-2\sqrt{2};1+\sqrt{2}\right);\left(-3+2\sqrt{2};1-\sqrt{2}\right)\)\(;\left(-3+\sqrt{5};\frac{1-\sqrt{5}}{2}\right);\left(-3-\sqrt{5};\frac{1+\sqrt{5}}{2}\right)\)

Ta có: x²y + xy - 2x² - 3x + 4 = 0

=> x²(y - 2) + x(y - 2) - (x + 1) = -5

=> (x² + x)(y - 2) - (x + 1) = -5

=> x(x + 1)(y - 2) - (x + 1) = -5

=> (x - 1)[x(y - 2) - 1] = -5

=>  x - 1; x(y - 2) - 1 \(\in\)Ư(-5) = {1; -1; 5; -5}

Với : x - 1 = 1           => x = 2

      x(y - 2)  - 1 = -5 => x(y - 2) = -4   => y - 2 = -2      => y = 0

x - 1 = -1                => x = 0

x(y - 2) - 1 = 5  => x(y - 2) = 6       (ktm vì x = 0)

x - 1 = 5                => x = 6

x(y - 2) - 1 = -1      => x(y - 2) = 0                 => y - 2 = 0          => y = 2

x - 1 = -5              => x = -4

x(y - 2) - 1 = 1    => x(y - 2) = 2              => y - 2 = -1/2             => y = 3/2

Vậy ...

NX: x = y = 0 là 1 nghiệm của hpt 

Với x ; y khác 0 thì chia cả 2 vế của hệ đã cho cho xy ta được

\(\hept{\begin{cases}y-\frac{2y}{x}+\frac{3x}{y}=0\\\frac{y}{x}+x+\frac{2}{y}=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y-\frac{2y}{x}=-\frac{3x}{y}\\x+\frac{2}{y}=-\frac{y}{x}\end{cases}}\)

 Nhân 2 vế của hệ trên lại ta đc

\(\left(y-\frac{2y}{x}\right)\left(x+\frac{2}{y}\right)=3\)

\(\Leftrightarrow xy-\frac{4}{xy}=3\)

\(\Leftrightarrow\orbr{\begin{cases}xy=4\\xy=-1\end{cases}}\)

Dễ rồi nha