Cho dãy số: 11; 14; 17;...;68

a, Dãy số trên là dãy số cách đều với khoảng cách là: 14 - 11 = 3

    Dãy số trên có số số hạng là: (68 - 11):3 + 1   = 20 (số)

b, Số thứ 100 của dãy số trên là:

    3 \(\times\)(100 - 1) + 11 = 308

  Đáp số: a, 20

                b, 308

a) Ta thấy mỗi số của dãy số trên đều cách đều nhau 3 đơn vị

=> Số số hạng của dãy số trên là:

  \(\left(68-11\right)\div3+1=20\) ( số hạng )

b) Ta thấy :

Số hạng thứ 2: \(14=11+3=11+\left(2-1\right)\times3\) 

Số hạng thứ 3: \(17=11+6=11+\left(3-1\right)\times3\) 

=> Số hạng thứ 100 là \(11+\left(100-1\right)\times3=308\)

a) Ta có số hạng tổng quát của dãy số \({u_n} = 5n + 1\;\left( {n\; \in {N^*}} \right)\).

b) Các số hạng của dãy số là: 6; 11; 16; 21; 26.

Số hạng đầu của dãy số là: 6 và số hạng cuối của dãy số là 26.

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:

u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15

Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.

b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:

n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10

Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.

u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5

Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.

b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:

(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1

Vậy số hạng thứ mấy có giá trị 137137 là u1.

a: cứ mỗi số tăng lên 3 đơn vị

a,  Quy luật dãy số trên: mỗi chữ số cách nhau 3 đơn vị.

b, A = {2 ; 5 ; 8 ; 11 ; 14 ; 17 ; 20 ; 23 ; 26 ; 29}

c, Dựa theo quy luật tính số hạng ta có:

        2 + (20-1) . 3 = 59

⇒ số hạng thứ 20 của dãy là 59 

Số 10 không phải là số hạng của dãy số trên.

Vì :

Tổng các số khi cộng cho 3 của dãy số trên không có tổng nào bằng 10 vậy nên 10 không phải số hạng của dãy số trên.

Tổng của 20 số hạng đầu tiên của dãy số là:

    (59 + 2) . 20 : 2 = 610

thanks

Chọn D.

Ta có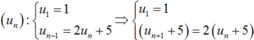 

Đặt: v_n = u_n + 5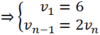

Khi đó ta được dãy mới; là cấp số nhân với : v₁ = 6; q = 2

⇒ v₂₀₁₈ = 2²⁰¹⁷.v₁ = 6.2²⁰¹⁷ ⇒ u₂₀₁₈ = 6.2²⁰¹⁷ – 5.

Đáp án D

Ta có:  u n : u 1 = 1 u n − 1 = 2 u n + 5 ⇒ u 1 = 1 u n + 1 + 5 = 2 u n + 5

Đặt:  v n = u n + 5 ⇒ v 1 = 6 v n − 1 = 2 v n

⇒ v 2018 = 2 2017 . v 1 = 6.2 2017 ⇒ u 2018 = 6.2 2017 − 5

Đáp án C

Phân tích  v n + 1 + k = 2 u n + k ⇒ k = 5 ⇒ u n + 1 + 5 = 2 u n + 5

Đặt 

v n = u n + 5 ⇒ v n + 1 = 2 v n C S N ⇒ v n = v 1 q n − 1 = u 1 + 5 .2 n − 1 = 6.2 n − 1

⇒ u n + 5 = 6.2 n − 1 ⇒ u 2018 = 6.2 2017 − 5

Chọn đáp án A.