Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

1:
Cách vẽ: Vẽ một đường thẳng vuông góc với một đọan thẳng cho trước tại trung điểm của đoạn thẳng đó

Có Am // Oy(gt)
=>góc xAm= góc AOy( 2 góc đồng vị)
mà góc xAn =1/2 góc xAm( An là tia phân giác góc xAm)
góc AOt = 1/2 góc AOy ( Ot là tia phân giác góc AOy)
=> góc xAn = góc AOt
mà 2 góc này ở vị trí đồng vị
=> An//Ot( dấu hiệu nhận biết 2 đường thẳng //)
b)
có An// Ot (cmt)
mà AH vuông góc vs Ot(gt)
=> AH vuông góc vs An ( từ vuông góc đến //)
=> góc HAn =90 độ
hay góc HAm + góc nAM = 90 độ (1)
Có góc OAH + góc HAn +góc xAn= góc OAx
mà góc OAx =180 độ(gt)
góc HAn = 90 độ (cmt)
=> góc OAH +90 độ + góc xAn = 180 độ
=> góc OAH + góc xAn = 180 độ - 90 độ = 90 độ
mà góc xAn = góc nAm ( An là tia phân giác góc xAm)
=> góc OAH + góc nAm = 90 độ (2)
từ (1) và (2) => góc HAm + góc nAm = góc OAH+ góc nAm (= 90 độ)
=> góc HAm = góc OAH
=> AH là tia phân giác góc OAm

Chọn hệ trục tọa độ Oxyz có gốc O ≡ A; 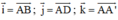
⇒ A(0; 0; 0) ; B(1; 0; 0); C(1; 1; 0); D(0; 1; 0).
A’(0; 0; 1); B’(1; 0; 1); C’(1; 1; 1); D’(0; 1; 1).
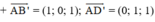
⇒ Vectơ pháp tuyến của (AB’D’) là:
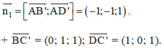
⇒ Vectơ pháp tuyến của (BC’D) là:
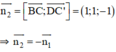
⇒ (AB’D’) // (BC’D).

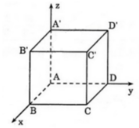
a: Ta có: xx'\(\perp\)AB
yy'\(\perp\)AB
Do đó: xx'//yy'
b: xx'//y'y
=>\(\widehat{ADC}=\widehat{C_1}\)(hai góc so le trong)
=>\(\widehat{C_1}=74^0\)
c: DE là phân giác của góc CDF
=>\(\widehat{FDE}=\dfrac{\widehat{FDC}}{2}=\dfrac{106^0}{2}=53^0\)
Xét ΔDEF có \(\widehat{x'FE}\) là góc ngoài tại F
nên \(\widehat{x'FE}=\widehat{FED}+\widehat{FDE}=70^0+53^0=123^0\)