Cho hình thang ABCD có đáy AB;CD. Biết AB=2cm; CD= 3cm
a. So sánh diện tích tam giác ABC và tam giác ACD
b. Tính diện tích tam giác ABC. Biết chiều cao hình thang là 3cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOBA và ΔODC có
góc OBA=góc ODC
góc BOA=góc DOC
=>ΔOBA đồng dạng với ΔODC
=>OB/OD=OA/OC=AB/CD=1/3
=>S ABO=1/3*S ABC
=>S BOC=2/3*S ABC
b: Kẻ CH vuông góc AB
=>S ABC=1/2*CH*AB
S ABCD=1/2*CH*(AB+CD)
=>S ABC/S ABCD=AB/(AB+CD)

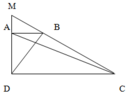
a. S A B C = 1 3 S A D C (Vì cùng chung chiều cao của hình thang ABCD; đáy AB = 1 3 DC)
b. S A B M = S A C M (Vì cùng chung đáy MA, chiều cao AB = 1 3 DC )
c. Theo phần a, ta có: S A B C = S A D C
Mà S A B C D = S A B C + S A D C
Nên S A B C = 1 1 + 3 S A B C D = 1 4 S A B C D
Do đó S A B C D = 64 × 1 4 = 16 ( c m 2 )
Theo phần b, ta có: S A B M = 1 3 S A C M
Mà S A C M = S M A B + S A B C
Nên S M A B = 1 3 - 1 S A B C = 1 2 S A B C
Do đó S M A B = 16 × 1 4 = 8 ( c m 2 )
a: Vì ABCD là hình thang
nên \(\dfrac{S_{ABC}}{S_{ACD}}=\dfrac{AB}{CD}=\dfrac{2}{3}\)
b: Diện tích hình thang ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\cdot3\cdot\left(2+3\right)=\dfrac{15}{2}\left(cm^2\right)\)
\(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{2}{3}\)
=>\(S_{ADC}=1,5\cdot S_{ABC}\)
\(S_{ABC}+S_{ADC}=S_{ABCD}\)
=>\(1,5\cdot S_{ABC}+S_{ABC}=7,5\)
=>\(2,5\cdot S_{ABC}=7,5\)
=>\(S_{ABC}=3\left(cm^2\right)\)