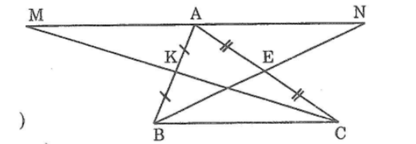
Cho tam giác ABC. Gọi E là trung điểm của AC, F là trung điểm của AB. Trên tia đối của tia EB lấy điểm M sao cho EM=EB. Trên tia đối của tia FC lấy điểm N sao cho FN=FC. Chứng minh:
a)Tam giác AME=Tam giác CBE
b)AM=BC và AM//BC
c)AM=AN
d)M,A,N thẳng hàng